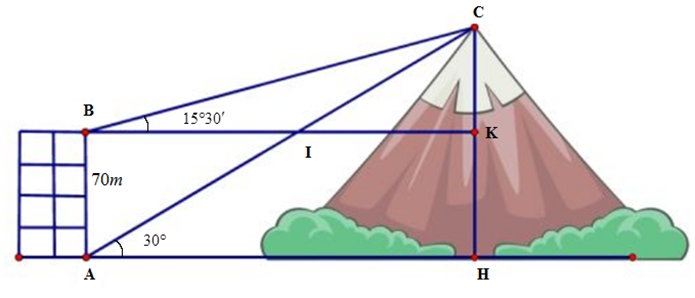
Từ hai vị trí \(A\) và \(B\) của một tòa nhà, người ta quan sát đỉnh \(C\) của ngọn núi. Biết rằng độ cao \(AB\) bằng \(70m\), phương nhìn \(AC\) tạo với phương nằm ngang góc \(30^\circ \). Phương nhìn \(BC\) tạo với phương nằm ngang góc \(15^\circ 30'\). Khi đó chiều cao của ngọn núi so với mặt đất (làm tròn đến hàng đơn vị) bằng
A. \(136m\).
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 10 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn B
Ta có: \(\widehat {CIK} = \widehat {CAH} = 30^\circ ;\widehat {BAC} = 60^\circ \); \(\widehat {BIC} = 180^\circ - \widehat {CIK} = 150^\circ \).
\(\widehat {BCA} = \widehat {BCI} = 180^\circ - \widehat {CBK} - \widehat {BIC} = 14^\circ 30'\).
Trong tam giác \(ABC\) ta có: \(\frac{{AB}}{{\sin \widehat {BCA}}} = \frac{{BC}}{{\sin \widehat {BAC}}} \Rightarrow BC = \frac{{AB.\sin \widehat {BAC}}}{{\sin \widehat {BCA}}}\).
Trong tam giác \(BCK\) ta có: \(CK = BC\sin \widehat {CBK} = \frac{{AB.\sin \widehat {BAC}.\sin \widehat {CBK}}}{{\sin \widehat {BCA}}}\).
Vậy đường cao khối chóp là: \(CH = CK + KH = CK + AB = \frac{{AB.\sin \widehat {BAC}.\sin \widehat {CBK}}}{{\sin \widehat {BCA}}} + AB \approx 135m\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
|
Trả lời |
1 |
0 |
|
|
Gọi là số tấn trục sắt và đinh ốc sản xuất trong ngày.
Số tiền lãi mỗi ngày: \(L(x,y) = 2x + y\) (triệu đồng).
Số giờ làm việc mỗi ngày của máy cắt: \[3x + y\] (giờ).
Số giờ làm việc mỗi ngày của máy tiện: \(x + y\) (giờ).
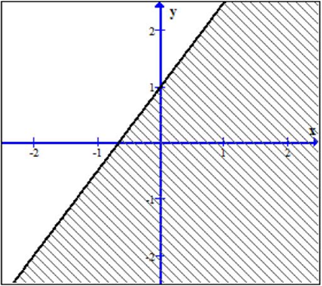
Ta có hệ phương trình: \(\left\{ \begin{array}{l}3x + y \le 6\\x + y \le 4\\x \ge 0\\y \ge 0\end{array} \right.\,\)
Bài toán trở thành: Trong các nghiệm của hệ bất phương trình \(\left( * \right)\), tìm nghiệm \[({x_0};{y_0})\] sao cho \[L\left( {x;y} \right) = 2x + y\] lớn nhất.
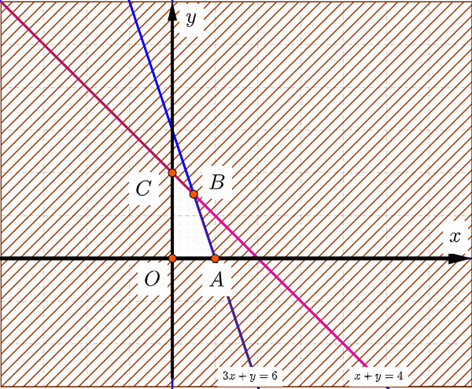
Miền nghiệm của \((*)\) là tứ giác \(OABC\)như hình vẽ với \(O(0;0),A(2;0),B(1;3),C(0;4)\).
Ta có: \(L(0;0) = 0,L(2;0) = 4,L(1,3) = 5,L(0,4) = 4\).
Suy ra: GTLN của \(L\left( {x;y} \right)\) bằng \(5\) khi \(\left( {x;y} \right) = \left( {1;3} \right)\)
Vậy một ngày xưởng nên sản xuất 1 tấn trục sắt và 3 tấn đinh ốc để tiền lãi cao nhất.
Khi đó \(a = 1,\;b = 3\;\)nên \(a + 3b = 10\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
|
Trả lời |
5 |
, |
7 |
4 |
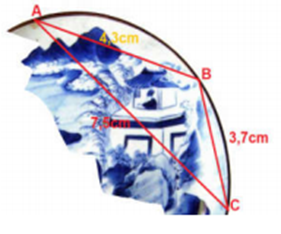
Bán kính \[R\] của chiếc đĩa bằng bán kính đường tròn ngoại tiếp tam giác\[ABC\].
Nửa chu vi của tam giác \[ABC\] là: \[p = \frac{{AB + BC + CA}}{2} = \frac{{4,3 + 3,7 + 7,5}}{2} = \frac{{31}}{4}\]cm.
Diện tích tam giác \[ABC\] là: \[S = \sqrt {p\left( {p - AB} \right)\left( {p - BC} \right)\left( {p - CA} \right)} \approx 5,2\]cm2.
Mà \[S = \frac{{AB.BC.CA}}{{4R}} \Rightarrow R = \frac{{AB.BC.CA}}{{4S}} \approx 5,74\]cm.
Câu 3
A. \(\frac{{2a}}{3}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập