(1,0 điểm) Từ độ cao \(55,8\,\,{\rm{m}}\) của tháp nghiêng Pisa nước Italia người ta thả một quả bóng cao su chạm xuống đất. Giả sử mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng \(\frac{1}{{10}}\) độ cao mà quả bóng đạt trước đó. Hỏi tổng độ dài hành trình của quả bóng được thả từ lúc ban đầu cho đến khi nó nằm yên trên mặt đất là bao nhiêu?

Từ giả thiết \(M\) là điểm trên đoạn \(BC\) sao cho \[MB = 2MC\] nên ta có \[\overrightarrow {BM} = \frac{1}{3}\overrightarrow {BC} \].

Đặt \[AB = x;{\rm{ }}AC = y\] ta có \[{x^2} + {y^2} = 4{a^2}\] (1) (Tam giác \(ABC\) vuông tại \(A\))

Mặt khác từ \[\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} = \overrightarrow {AB} + \frac{1}{3}\overrightarrow {BC} = \overrightarrow {AB} + \frac{1}{3}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) = \frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \].

Nên có \[\overrightarrow {AM} \cdot \overrightarrow {BC} = {a^2} \Leftrightarrow \left( {\frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} } \right)\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) = {a^2}\]

\[ \Leftrightarrow \frac{1}{3}{\overrightarrow {AC} ^2} - \frac{2}{3}{\overrightarrow {AB} ^2} = {a^2}\,\,{\rm{ }}\left( {{\rm{Do }}\overrightarrow {AB} \cdot \overrightarrow {AC} = 0} \right)\]

\[ \Leftrightarrow \frac{1}{3}{y^2} - \frac{2}{3}{x^2} = {a^2}\,\,\,(2)\]

Từ (1) và (2) ta có \[y = \frac{{a\sqrt {33} }}{3}\]. Vậy \[AC = \frac{{a\sqrt {33} }}{3}\].

Đáp án đúng là: B

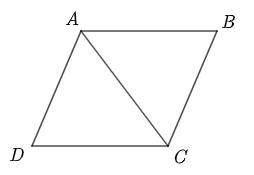
Vì \[ABCD\] là hình thoi nên \(AC\) là tia phân giác của góc \(BAD\).

Khi đó \(\widehat {BAC} = \frac{1}{2}\widehat {BAD} = 60^\circ \).

Tam giác \(ABC\) có \(AB = BC\) và \(\widehat {BAC} = 60^\circ \) nên tam giác \(ABC\) đều.

Do đó, \(AC = AB = BC = 2\) và \(\widehat {ACB} = 60^\circ \).

Ta có: \(\overrightarrow {AC} \cdot \overrightarrow {BC} = \left( { - \overrightarrow {CA} } \right) \cdot \left( { - \overrightarrow {CB} } \right) = \overrightarrow {CA} \cdot \overrightarrow {CB} \)\( = \left| {\overrightarrow {CA} } \right| \cdot \left| {\overrightarrow {CB} } \right| \cdot \cos \left( {\overrightarrow {CA} ,\,\,\overrightarrow {CB} } \right)\)

\( = CA \cdot CB \cdot \cos \widehat {ACB} = 2 \cdot 2 \cdot \cos 60^\circ = 2\).