Giả sử \(CD = h\) là chiều cao của tháp trong đó \(C\) là chân tháp. Chọn hai điểm \(A,B\) trên mặt đất sao cho ba điểm \(A,\,B,\,C\) thẳng hàng. Ta đo được \(AB = 24\,m\), \(\widehat {CAD} = 63^\circ \), \(\widehat {CBD} = 48^\circ \) (tham khảo hình vẽ).
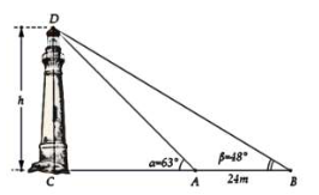
Tính gần đúng chiều cao \(h\) của khối chóp.
Giả sử \(CD = h\) là chiều cao của tháp trong đó \(C\) là chân tháp. Chọn hai điểm \(A,B\) trên mặt đất sao cho ba điểm \(A,\,B,\,C\) thẳng hàng. Ta đo được \(AB = 24\,m\), \(\widehat {CAD} = 63^\circ \), \(\widehat {CBD} = 48^\circ \) (tham khảo hình vẽ).
Tính gần đúng chiều cao \(h\) của khối chóp.
Câu hỏi trong đề: Bộ 10 đề thi Giữa kì 1 Toán 10 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Ta có: \(\widehat {BDA} = \widehat {CAD} - \widehat {CBD} = 63^\circ - 48^\circ = 15^\circ \)
Áp dụng định lí sin trong tam giác \(ABD\), có:
\(\frac{{AB}}{{\sin ADB}} = \frac{{AD}}{{\sin ABD}}\)
\( \Leftrightarrow \frac{{24}}{{\sin 15^\circ }} = \frac{{AD}}{{\sin 48^\circ }}\)
\( \Leftrightarrow AD = \frac{{24.\sin 48^\circ }}{{\sin 15^\circ }} \approx 68,9\).
Xét tam giác vuông \(ACD\) vuông tại \(C\), ta có:
\(CD = \sin CAD.AD \approx \sin 63^\circ .68,9 \approx 61,4.\)
Vậy chiều cao của tháp khoảng \(61,4\,\,m\).
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
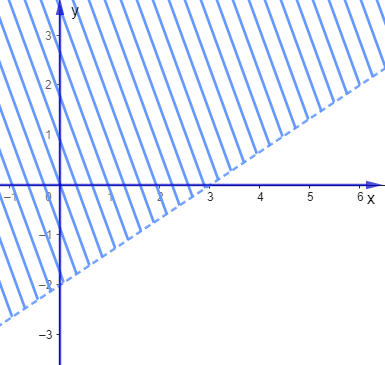
Gọi số \(ha\) trồng dứa và trồng củ đậu lần lượt là \(x\) và \(y\) (\(ha\)), \(\left( {x,y \ge 0} \right)\).
Khi đó ta có: \(x + y \le 8\).
Tổng số công trồng \(x\left( {ha} \right)\) dứa và \(y\left( {ha} \right)\) củ đậu thỏa mãn không quá \(180\) công là: \(20x + 30y \le 180\) hay \(2x + 3y \le 18\).
Khi đó ta có hệ bất phương trình: \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 8\\2x + 3y \le 18\end{array} \right.\).
Miền nghiệm của hệ bất phương trình là miền trong của tứ giác \(OABC\) với \(O\left( {0;\,\,0} \right)\), \(A\left( {0;\,\,6} \right)\), \(B\left( {6;\,\,2} \right)\), \(D\left( {8;\,\,0} \right)\).
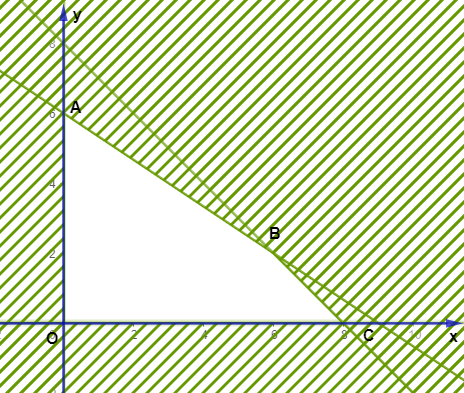
Tiền thu được khi trồng \(x\left( {ha} \right)\) dứa và \(y\left( {ha} \right)\) củ đậu là: \(F\left( {x;\,\,y} \right) = 5x + 4y\) (triệu đồng).
Ta có:
Tại \(O\left( {0;\,\,0} \right)\) có \(F\left( {0;\,\,0} \right) = 5.0 + 4.0 = 0\);
Tại \(A\left( {0;\,\,6} \right)\) có \(F\left( {0;\,\,6} \right) = 5.0 + 4.6 = 24\);
Tại \(B\left( {6;\,\,2} \right)\) có \(F\left( {6;\,\,2} \right) = 5.6 + 4.2 = 38\);
Tại \(D\left( {8;\,\,0} \right)\) có \(F\left( {8;\,\,0} \right) = 5.8 + 4.0 = 40\).
Vậy để thu được nhiều tiền nhất hộ nông dân đó cần trồng \(8\,\,ha\) dứa và \(0\,\,ha\) củ đậu.
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Gọi \(x\) và \(y\) lần lượt là số phút Thảo dùng để đọc sách \(A\) và sách \(B\)\[\left( {x\,,\,\,y \in \mathbb{N}} \right)\]
Mỗi ngày bạn Thảo đều dành không quá 30 phút để đọc nên ta có: \(x + y \ge 30\).
Một phút Thảo đọc được \(\frac{3}{2}x\) trang sách \(A\).
Một phút Thảo đọc được \(2y\) trang sách \(B\).
Số trang sách Thảo đọc trong một ngày là: \(\frac{3}{2}x + 2y\) (trang).
Mỗi ngày Thảo đọc được ít nhất 35 trang nên ta có: \(\frac{3}{2}x + 2y \le 35\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập