(1 điểm) Bạn Nam đứng ở chân một tòa nhà, Nam nhìn hướng lên \(24^\circ \) thì thấy ngọn của một cái cây. Và nếu Nam đứng ở đỉnh của tòa nhà ấy, biết tòa nhà cao 155 m, Nam nhìn hướng xuống một góc \(60^\circ \) so với phương nằm ngang để thấy ngọn của cái cây đó. Tính chiều cao của cái cây (làm tròn đến hàng phần trăm).
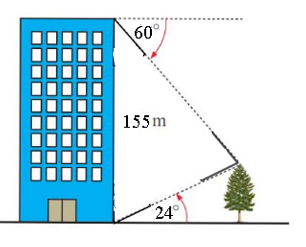
(1 điểm) Bạn Nam đứng ở chân một tòa nhà, Nam nhìn hướng lên \(24^\circ \) thì thấy ngọn của một cái cây. Và nếu Nam đứng ở đỉnh của tòa nhà ấy, biết tòa nhà cao 155 m, Nam nhìn hướng xuống một góc \(60^\circ \) so với phương nằm ngang để thấy ngọn của cái cây đó. Tính chiều cao của cái cây (làm tròn đến hàng phần trăm).

Quảng cáo
Trả lời:
Kí hiệu như hình vẽ trên với \(A\), \(C\) lần lượt là đỉnh và chân của tòa nhà; \(B\) và \(D\) lần lượt là đỉnh và gốc của cây.
Xét tam giác \(ABC\)
Do \(\left\{ \begin{array}{l}\widehat {BCD} = 24^\circ \\\widehat {BCD} + \widehat {ACB} = 90^\circ \end{array} \right. \Rightarrow \widehat {ACB} = 66^\circ \).
Do \(\left\{ \begin{array}{l}\widehat {xAB} = 60^\circ \\\widehat {xAB} + \widehat {CAB} = 90^\circ \end{array} \right. \Rightarrow \widehat {CAB} = 30^\circ \).
Suy ra \(\widehat {ABC} = 180^\circ - \left( {66^\circ + 30^\circ } \right) = 84^\circ \).
Áp dụng định lí sin ta có:
\(\frac{{BC}}{{\sin 30^\circ }} = \frac{{AC}}{{\sin 84^\circ }} \Rightarrow BC = \frac{{AC \cdot \sin 30^\circ }}{{\sin 84^\circ }} = \frac{{155 \cdot \sin 30^\circ }}{{\sin 84^\circ }} \approx 77,93\) (m).
Xét tam giác \(CBD\) vuông tại \(D\)
Ta có: \(\sin \widehat {BCD} = \frac{{BD}}{{BC}} \Rightarrow \sin 24^\circ \approx \frac{{BD}}{{77,93}} \Rightarrow BD \approx 77,93 \cdot \sin 24^\circ \approx 31,70\) (m)
Vậy chiều cao của cái cây khoảng 31,70 mét.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là: B
Xét tam giác đều \(ABC\) cạnh bằng 4.
Ta có: \(AB = AC = 4\, \Rightarrow \left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {AC} } \right| = 4\,\)
\(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {BAC} = 60^\circ \Rightarrow \cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \cos 60^\circ = \frac{1}{2}\).
Vậy \(\overrightarrow {AB} \cdot \overrightarrow {AC} = \left| {\overrightarrow {AB} } \right| \cdot \left| {\overrightarrow {AC} } \right| \cdot \cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = 4 \cdot 4 \cdot \frac{1}{2} = 8\).
Câu 2
Lời giải
Đáp án đúng là: D
Công thức Hê – rông tính diện tích tam giác: \(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \).
Vậy khẳng định \(S = \sqrt {p\left( {p + a} \right)\left( {p + b} \right)\left( {p + c} \right)} \) là sai.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.