(1,0 điểm) Hai lớp 10A và 10B của một trường Trung học phổ thông cùng làm bài thi môn Toán, chung một đề thi. Kết quả thi được trình bày ở hai bảng tần số sau đây:
Lớp 10A:
Điểm
3
5
6
7
8
9
10
Số học sinh
7
9
3
3
7
12
4
n = 45
Lớp 10B:
Điểm
4
5
6
7
8
9
10
Số học sinh
6
6
7
8
9
5
4
n = 45
Hỏi lớp nào có kết quả thi đồng đều hơn?
(1,0 điểm) Hai lớp 10A và 10B của một trường Trung học phổ thông cùng làm bài thi môn Toán, chung một đề thi. Kết quả thi được trình bày ở hai bảng tần số sau đây:
Lớp 10A:
|
Điểm |
3 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
Số học sinh |
7 |
9 |
3 |
3 |
7 |
12 |
4 |
n = 45 |
Lớp 10B:
|
Điểm |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
Số học sinh |
6 |
6 |
7 |
8 |
9 |
5 |
4 |
n = 45 |
Hỏi lớp nào có kết quả thi đồng đều hơn?
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 10 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Để xét xem kết quả thi của lớp nào đồng đều hơn thì ta đi so sánh phương sai của điểm thi hai lớp.
+) Điểm thi trung bình lớp 10A là:
\[{x_{10A}} = \frac{{3.7 + 5.9 + 6.3 + 7.3 + 8.7 + 9.12 + 10.4}}{{45}} = \frac{{103}}{{15}} \approx 6,87\].
Phương sai mẫu số liệu của lớp 10A là:
\[\begin{array}{l}S_{10A}^2 = \frac{1}{{45}}\left( {{{7.3}^2} + {{9.5}^2} + {{3.6}^2} + {{3.7}^2} + {{7.8}^2} + {{12.9}^2} + {{4.10}^2}} \right) - \bar x_{10A}^2\\S_{10A}^2 = \frac{{2363}}{{45}} - {\left( {\frac{{103}}{{15}}} \right)^2} = \frac{{134}}{{25}} = 5,36.\end{array}\]
+) Điểm thi trung bình lớp 10B là:
\[{x_{10A}} = \frac{{4.6 + 5.6 + 6.7 + 7.8 + 8.9 + 9.5 + 10.4}}{{45}} = \frac{{103}}{{15}} \approx 6,87\].
Phương sai mẫu số liệu của lớp 10B là:
\[\begin{array}{l}S_{10B}^2 = \frac{1}{{45}}\left( {{{6.4}^2} + {{6.5}^2} + {{7.6}^2} + {{8.7}^2} + {{9.8}^2} + {{5.9}^2} + {{4.10}^2}} \right) - \bar x_{10B}^2\\S_{10B}^2 = \frac{{757}}{{15}} - {\left( {\frac{{103}}{{15}}} \right)^2} = \frac{{746}}{{225}} \approx 3,32.\end{array}\]
+) Vì \[3,32 < 5,36\] nên lớp 10B có kết quả thi đồng đều hơn lớp 10A.
Đang tải chế độ Học...
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
Ta có: \[\widehat {BAC} = \widehat {BAD} - \widehat {DAC} = 10^\circ \].
\[\widehat {ABD} = 180^\circ - \left( {\widehat {BAD} + \widehat {ADC}} \right) = 180^\circ - \left( {50^\circ + 90^\circ } \right) = 40^\circ \]
Áp dụng định lý sin trong tam giác \[ABC\], có:
\[\begin{array}{l}\frac{{BC}}{{\sin \widehat {BAC}}} = \frac{{AC}}{{\sin \widehat {ABC}}}\\ \Rightarrow AC = \frac{{BC.\sin \widehat {ABC}}}{{\sin \widehat {BAC}}} = \frac{{5.\sin 40^\circ }}{{\sin 10^\circ }} \approx 18,5.\end{array}\]
Xét tam giác vuông \[ADC\], có:
\[\widehat {CAD} = \frac{{CD}}{{AC}} \Rightarrow CD = AC.\sin \widehat {CAD} = 18,5.\sin 40^\circ \approx 11,9\].
Vậy \[CH = CD + DH = 11,9 + 7 = 18,9\left( m \right) \Rightarrow CH \approx 19m\].
Lời giải
Hướng dẫn giải
Gọi số tiền mà doanh nghiệp A dự định giảm giá là \(x\) ( triệu đồng) \(\left( {0 \le x \le 4} \right)\).
Tiền lãi khi bán được một xe là: \(31 - x - 27 = 4 - x\)(triệu đồng).
Số lượng xe bán được khi đã giảm giá là: \(600 + 200x\) (xe).
Lợi nhuận cửa hàng thu được là: \(\left( {600 + 200x} \right)\left( {4 - x} \right) = - 200{x^2} + 200x + 2\,\,400\)(triệu đồng).
Xét hàm số bậc hai \(y = - 200{x^2} + 200x + 2\,\,400\), có:
Đỉnh \(I\) có tọa độ: \({x_I} = - \frac{b}{{2a}} = - \frac{{200}}{{2.\left( { - 200} \right)}} = \frac{1}{2}\); \({y_I} = - \frac{\Delta }{{4a}} = - \frac{{1\,\,960\,\,000}}{{4.\left( { - 200} \right)}} = 2\,\,450\).
Hay \(I\left( {\frac{1}{2};2\,\,450} \right)\)
Ta có bảng biến thiên:
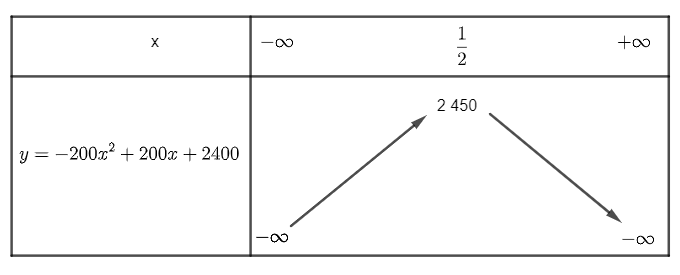
Dựa vào bảng biến thiên ta thấy, hàm số đạt giá trị lớn nhất là \(2\,450\) khi x = \(\frac{1}{2}\).
Vậy doanh nghiệp phải bán với giá \(30,5\) triệu đồng để lợi nhuận thu được là cao nhất.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Một cửa hàng bán quần áo thời trang đang mở một chương trình khuyến mãi trong vòng 4 ngày, biết rằng số sản phẩm bán được mỗi ngày đều tăng khoảng \[30\% \] so với ngày trước đó. Nhân viên bán hàng đã thống kê số sản phẩm bán được mỗi ngày như bảng dưới đây:
Chọn phát biểu đúng:
|
Ngày |
1 |
2 |
3 |
4 |
|
Số sản phẩm bán được |
50 |
66 |
93 |
115 |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập