Từ vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của một ngọn núi. Biết rằng độ cao AB là 70m, phương nhìn AC tạo với phương nằm ngang góc\(30^\circ \), phương nhìn BC tạo với phương nằm ngang góc \(15^\circ 30'\). Hỏi ngọn núi đó cao bao nhiêu mét so với mặt đất? (Làm tròn kết quả đến hàng phần mười).
Từ vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của một ngọn núi. Biết rằng độ cao AB là 70m, phương nhìn AC tạo với phương nằm ngang góc\(30^\circ \), phương nhìn BC tạo với phương nằm ngang góc \(15^\circ 30'\). Hỏi ngọn núi đó cao bao nhiêu mét so với mặt đất? (Làm tròn kết quả đến hàng phần mười).
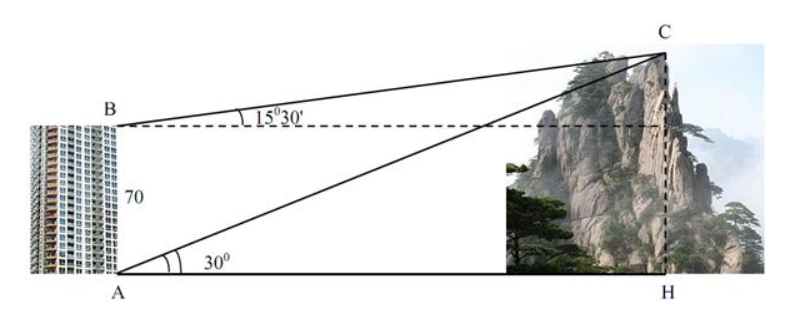
Từ vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của một ngọn núi. Biết rằng độ cao AB là 70m, phương nhìn AC tạo với phương nằm ngang góc\(30^\circ \), phương nhìn BC tạo với phương nằm ngang góc \(15^\circ 30'\). Hỏi ngọn núi đó cao bao nhiêu mét so với mặt đất? (Làm tròn kết quả đến hàng phần mười).
Từ vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của một ngọn núi. Biết rằng độ cao AB là 70m, phương nhìn AC tạo với phương nằm ngang góc\(30^\circ \), phương nhìn BC tạo với phương nằm ngang góc \(15^\circ 30'\). Hỏi ngọn núi đó cao bao nhiêu mét so với mặt đất? (Làm tròn kết quả đến hàng phần mười).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn B
Từ hình vẽ ta có \[\widehat {ABC} = 90^\circ + 15^\circ 30' = 105^\circ 30'\].
Xét tam giác \[ABC\] có \[\widehat {CAB} = 60^\circ \], \[\widehat {ABC} = 105^\circ 30'\] ta có
\[\widehat {CAB} + \widehat {ABC} + \widehat {ACB} = 180^\circ \] (Định lý tổng ba góc trong tam giác)
Áp dụng định lý sin trong tam giác \[ABC\], ta có \[\frac{{AC}}{{\sin \widehat {ABC}}} = \frac{{AB}}{{\sin \widehat {ACB}}}\]
\[ \Rightarrow AC = \frac{{AB\sin \widehat {ABC}}}{{\sin \widehat {ACB}}} = \frac{{70.\sin 105^\circ 30'}}{{\sin 14^\circ 30'}} \approx 269,4\](m).
Tam giác \[ACH\] vuông tại \[H\] nên ta có \[CH = AC.\sin \widehat {CAH} \approx 269,4.\sin 30^\circ \approx 134,7\] (m).
Vậy ngọn núi cao khoảng \[135\] (m) so với mặt đất.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn B
· \(A \cap B = \emptyset \Leftrightarrow m + 2 < 1 \Leftrightarrow m < - 1\).
· \(A \cap B = \emptyset \Leftrightarrow 3 \le m \Leftrightarrow m \ge 3\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn A
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập