a) Cho góc \(x\) thỏa mãn \(0^\circ \le x \le 180^\circ .\)
Rút gọn biểu thức \(P = \sin \left( {90^\circ - x} \right){\rm{cos}}\,x + \sin \left( {180^\circ - x} \right)\sin \,x.\)
b) Hai tàu du lịch xuất phát từ hai thành phố cảng \(A\) và \(B\) cách nhau \(200\,(km)\) đến đảo \(C\) như hình minh họa.
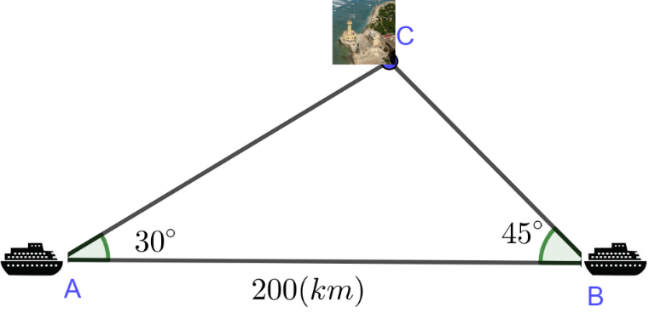
Biết \(\widehat {CAB} = 30^\circ ;\,\,\widehat {CBA} = 45^\circ .\) Tàu 1 ở thành phố \(A\) khởi hành lúc 8h và chuyển động đều với vận tốc \(80\,(km/h)\). Tàu 2 ở thành phố \(B\) muốn đến đảo \(C\) cùng lúc với tàu 1 thì phải khởi hành lúc mấy giờ biết tàu 2 chuyển động đều cùng vận tốc \(80\,(km/h)\)(kết quả làm tròn đến hai chữ số sau dấu phẩy thập phân).
a) Cho góc \(x\) thỏa mãn \(0^\circ \le x \le 180^\circ .\)
Rút gọn biểu thức \(P = \sin \left( {90^\circ - x} \right){\rm{cos}}\,x + \sin \left( {180^\circ - x} \right)\sin \,x.\)
b) Hai tàu du lịch xuất phát từ hai thành phố cảng \(A\) và \(B\) cách nhau \(200\,(km)\) đến đảo \(C\) như hình minh họa.
Biết \(\widehat {CAB} = 30^\circ ;\,\,\widehat {CBA} = 45^\circ .\) Tàu 1 ở thành phố \(A\) khởi hành lúc 8h và chuyển động đều với vận tốc \(80\,(km/h)\). Tàu 2 ở thành phố \(B\) muốn đến đảo \(C\) cùng lúc với tàu 1 thì phải khởi hành lúc mấy giờ biết tàu 2 chuyển động đều cùng vận tốc \(80\,(km/h)\)(kết quả làm tròn đến hai chữ số sau dấu phẩy thập phân).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
a) Ta có \(P = \sin \left( {90^\circ - x} \right){\rm{cos}}\,x + \sin \left( {180^\circ - x} \right)\sin \,x\)
\( = \cos x.\cos x + \sin x.\sin x\)\( = {\cos ^2}x + {\sin ^2}x = 1\).
b) Ta có \(\widehat {BAC} = 180^\circ - 30^\circ - 45^\circ = 105^\circ \)(Theo định lý tổng ba góc trong tam giác).
Áp dụng định lý sin vào tam giác ABC, ta có
\(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} \Leftrightarrow \frac{{200}}{{\sin 105^\circ }} = \frac{{BC}}{{\sin 30^\circ }} = \frac{{AC}}{{\sin 45^\circ }}\)
\( \Rightarrow \left\{ \begin{array}{l}AC \simeq 146,41\\BC \simeq 103,53\end{array} \right.\)
* Thời gian tàu \(1\) đi từ A đến C là: \(1,83\)(h) = \(1\)h \(50\) phút.
* Thời điểm tàu \(1\) đến C là: \(9\)h \(50\) phút.
* Thời gian tàu \(2\) đi từ B đến C là \(1,29\)(h) = \(1\)h \(17\) phút.
* Thời điểm xuất phát của tàu \(2\)là: \(8\)h \(33\) phút.a
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi cuối kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn B
· \(A \cap B = \emptyset \Leftrightarrow m + 2 < 1 \Leftrightarrow m < - 1\).
· \(A \cap B = \emptyset \Leftrightarrow 3 \le m \Leftrightarrow m \ge 3\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn A
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập