(1 điểm) Một phân xưởng có hai máy chuyên dụng M1 và M2 để sản xuất hai loại sản phẩm A và B theo đơn đặt hàng. Nếu sản xuất được một tấn sản phẩm loại A thì phân xưởng nhận được số tiền lãi là 2 triệu đồng. Nếu sản xuất được một tấn sản phẩm loại B thì phân xưởng nhận được số tiền lãi là 1,6 triệu đồng. Muốn sản xuất một tấn sản phẩm loại A, người ta phải dùng máy M1 trong 3 giờ và máy M2 trong 1 giờ. Muốn sản xuất một tấn sản phẩm loại B, người ta phải dùng máy M1 trong 1 giờ và máy M2 trong 1 giờ. Một máy không thể dùng để sản xuất đồng thời hai loại sản phẩm. Máy M1 làm việc không quá 6 giờ một ngày và máy M2 làm việc không quá 4 giờ một ngày.
a. Hãy lập và giải hệ bất phương trình biểu diễn các yếu tố trong đề bài.
b. Hỏi số tiền lãi lớn nhất mà phân xưởng này có thể thu được trong một ngày là bao nhiêu?
(1 điểm) Một phân xưởng có hai máy chuyên dụng M1 và M2 để sản xuất hai loại sản phẩm A và B theo đơn đặt hàng. Nếu sản xuất được một tấn sản phẩm loại A thì phân xưởng nhận được số tiền lãi là 2 triệu đồng. Nếu sản xuất được một tấn sản phẩm loại B thì phân xưởng nhận được số tiền lãi là 1,6 triệu đồng. Muốn sản xuất một tấn sản phẩm loại A, người ta phải dùng máy M1 trong 3 giờ và máy M2 trong 1 giờ. Muốn sản xuất một tấn sản phẩm loại B, người ta phải dùng máy M1 trong 1 giờ và máy M2 trong 1 giờ. Một máy không thể dùng để sản xuất đồng thời hai loại sản phẩm. Máy M1 làm việc không quá 6 giờ một ngày và máy M2 làm việc không quá 4 giờ một ngày.
a. Hãy lập và giải hệ bất phương trình biểu diễn các yếu tố trong đề bài.
b. Hỏi số tiền lãi lớn nhất mà phân xưởng này có thể thu được trong một ngày là bao nhiêu?
Quảng cáo
Trả lời:
Giải bởi Vietjack
a. Gọi \[x\](tấn) là khối lượng sản phẩm \[A\] sản xuất trong một ngày \[ \Rightarrow x \ge 0\].
Gọi \[y\](tấn) là khối lượng sản phẩm \[B\] sản xuất trong một ngày \[ \Rightarrow y \ge 0\].
Thời gian máy \[{M_1}\] sản xuất trong 1 ngày tối đa 6 giờ \[ \Rightarrow 3x + y \le 6\].
Thời gian máy \[{M_2}\] sản xuất trong 1 ngày tối đa 4 giờ \[ \Rightarrow x + y \le 4\].
Vậy \[x,y\] thỏa hệ bất phương trình \[\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\3x + y \le 6\\x + y \le 4\end{array} \right.\] (*).
Lần lượt vẽ các đường thẳng \[{d_1}:x = 0\] ; \[{d_2}:y = 0\] ; \[{d_3}:3x + y = 6\] ; \[{d_4}:x + y = 4\] lên hệ trục tọa độ \[Oxy\]
Ta có miền nghiệm của hệ bất phương trình (*) là hình tứ giác OABC, kể cả 4 cạnh OA, AB, BC, CO như hình vẽ.
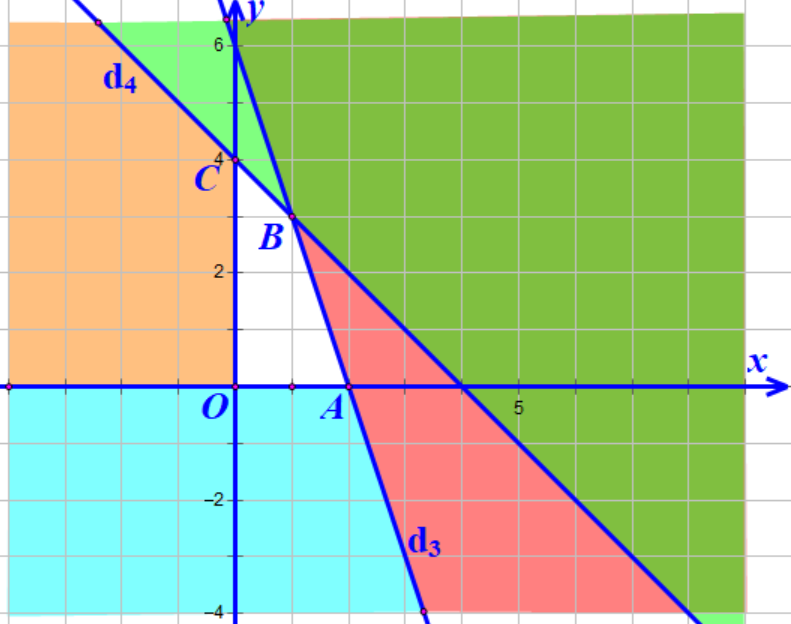
b. Tiền lãi thu được trong 1 ngày là \[T = 2x + 1,6y\].
Tính tọa độ các điểm \[{\rm{O}}(0;0),{\rm{ A(2;0), B(1;3), C(0;4)}}\]
Thay tọa độ điểm \[{\rm{O}}(0;0)\] vào \[T = 2x + 1,6y\] ta được \[T = 0\].
Thay tọa độ điểm \[{\rm{A(2;0)}}\] vào \[T = 2x + 1,6y\] ta được \[T = 4\].
Thay tọa độ điểm \[{\rm{B(1;3)}}\] vào \[T = 2x + 1,6y\] ta được \[T = 6,8\].
Thay tọa độ điểm \[{\rm{C(0;4)}}\] vào \[T = 2x + 1,6y\] ta được \[T = 6,4\].
Vậy số tiền lãi lớn nhất thu được trong 1 ngày là \[{\rm{6,8}}\] (triệu đồng).
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Tập xác định \[D = \mathbb{R}\].
Tọa độ đỉnh \[I\left( {1; - 3} \right)\].
Trục đối xứng \[x = 1\]
Hệ số \[a = 2 > 0\] nên ta có bảng biến thiên như sau:
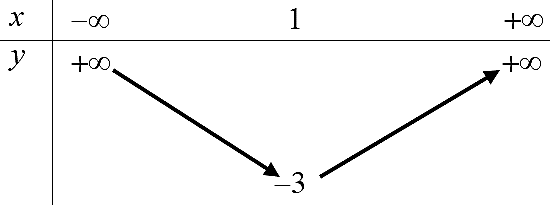
Hàm số đồng biến trên \[(1; + \infty )\], nghịch biến trên \[( - \infty ;1)\].
Điểm đặc biệt:
|
\[x\] |
\[ - 1\] |
0 |
1 |
\[2\] |
3 |
|
\[y\] |
\[5\] |
\[ - 1\] |
3 |
\[ - 1\] |
5 |
Đồ thị có bề lõm hướng lên
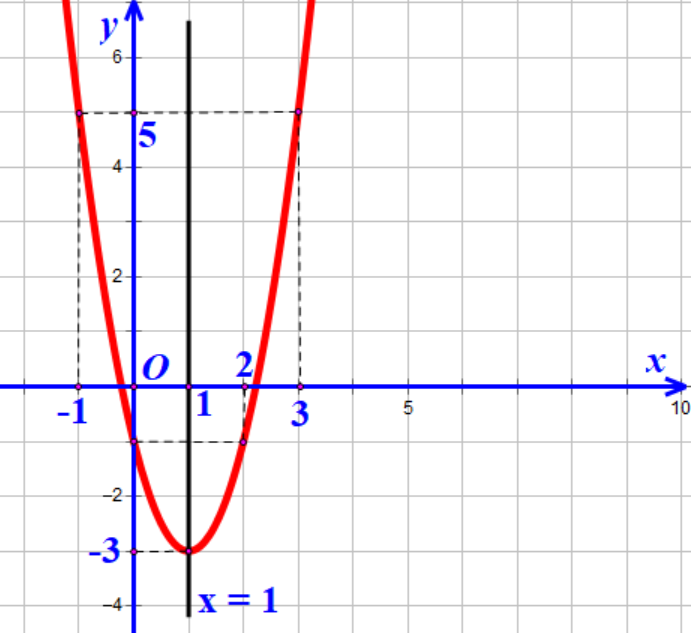
Câu 2
A. \[D = \left( { - \infty ;\frac{4}{3}} \right)\].
B. \[D = \left[ {\frac{4}{3}; + \infty } \right)\].
C. \[D = \left[ {\frac{2}{3};\frac{3}{4}} \right)\].
D. \[D = \left[ {\frac{3}{2};\frac{4}{3}} \right)\].
Lời giải
Chọn A
Điều kiện: \(4 - 3x > 0 \Leftrightarrow x < \frac{4}{3}\).
Tập xác định \[D = \left( { - \infty ;\frac{4}{3}} \right)\].
Câu 3
A. \[\left( { - 2;1} \right)\].
B. \[\left( {0;1} \right)\].
C. \[\left( {0;0} \right)\].
D. \[\left( {3; - 7} \right)\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(I\left( {\frac{1}{3};\, - \frac{2}{3}} \right)\).
B. \(I\left( {\frac{1}{3};\,\frac{2}{3}} \right)\)
C. \(I\left( {0;1} \right)\).
D. \(I\left( { - \frac{1}{3};\,\frac{2}{3}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\left\{ {a;b;c;d} \right\} \supset A\).
B. \(\left\{ a \right\} \supset A\).
C. \(\left\{ {a;\,c;d} \right\} \subset A\).
D. \(\emptyset \subset A\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[0\].
B. \( - \frac{3}{4}\).
C. \(\frac{1}{2}\).
D. \[1\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\frac{{11}}{4}\).
B. \(\frac{{15}}{4}\).
C. \(\frac{{13}}{4}\).
D. \(\frac{7}{4}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập