Tại một xã miền núi, có ba ngôi làng \(A,B,C\). Nhằm tạo điều kiện cho những trẻ em ở cả ba ngôi làng đều được đi học, nên người ta dự định xây một trường học \(X\) ở một vị trí thuận lợi và cách đều ba ngôi làng \(\left( {XA = XB = XC} \right)\). Đặt hệ trục tọa độ \(Oxy\), người ta xác định được tọa độ của ba ngôi làng lần lượt tương ứng với ba điểm \(A\left( {0;0} \right),B\left( {8;4} \right),C\left( {7;7} \right)\) (đơn vị trên mỗi trục là 1 kilômét). Giả sử vị trí trường học cần xây dựng là điểm \(X\left( {a;b} \right)\). Tính \(a + b\).

Có \(\overrightarrow {MB} \) và \(\overrightarrow {MC} \) ngược hướng và \(MB = 4MC\) nên \(\overrightarrow {MB} = - 4\overrightarrow {MC} \). Suy ra \(\overrightarrow {BM} = \frac{4}{5}\overrightarrow {BC} \).

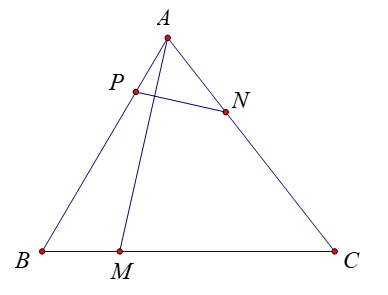
Khi đó \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} = \overrightarrow {AB} + \frac{4}{5}\overrightarrow {BC} = \overrightarrow {AB}  + \frac{4}{5}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right)\)\( = \frac{1}{5}\overrightarrow {AB} + \frac{4}{5}\overrightarrow {AC} \).

Suy ra \(m = \frac{1}{5};n = \frac{4}{5}\). Vậy \(6m + n = 2\).

Ta có \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \).

\(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} = 2 \cdot \frac{3}{2}\overrightarrow {AG} = 3\overrightarrow {AG} \).

\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \).

\(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \). Chọn B.