Bạn An muốn chọn mua một chiếc đồng hồ đeo tay. Có 3 kiểu mặt đồng hồ đeo tay là mặt đính đá, mặt dạng kính cong và mặt lộ cơ. Có 2 kiểu dây là dây da và dây kim loại. Hỏi An có bao nhiêu cách chọn một chiếc đồng hồ gồm một mặt và một dây?
A. \[9\].
Quảng cáo
Trả lời:
Đáp án đúng là C
Có 3 cách chọn mặt đồng hồ và 2 cách chọn dây đồng hồ
Áp dụng quy tắc nhân, ta có số cách chọn một chiếc đồng hồ là: \(3.2 = 6\)(cách).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
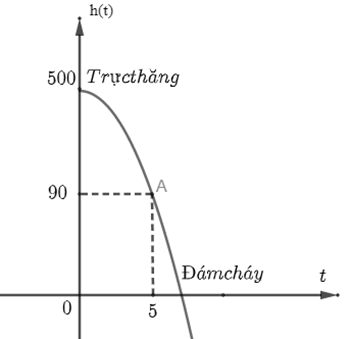
Chọn hệ trục \(Oth\) như hình vẽ với gốc tọa độ \(O\) là vị trí trên mặt đất thẳng đứng với trực thăng.
Xét phương trình parabol \(\left( P \right):h\left( t \right) = a{t^2} + bt + c,\,\,a \ne 0\).
Theo giả thiết ta có \(S\left( {0;500} \right)\)và đi qua điểm\(A\left( {5;90} \right)\).
Đỉnh \(S\left( {0;500} \right)\) của \(\left( P \right)\) nằm trên trục tung nên \(\left( P \right):h\left( t \right) = a{t^2} + 500.\)
Mặt khác, \(A\left( {5;90} \right) \in \left( P \right) \to a = - 16,4\). Từ đây ta được phương trình \(\left( P \right):h\left( t \right) = - 16,4{t^2} + 500.\)
Khi nước chạm đất ta được: \(\left\{ {\begin{array}{*{20}{l}}{t > 0}\\{h\left( t \right) = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{t > 0}\\{ - 16,4{t^2} + 500 = 0}\end{array}} \right. \Leftrightarrow t = \frac{{25\sqrt {82} }}{{41}}\).
Vậy \(\left\{ \begin{array}{l}b = 82\\c = 41\end{array} \right. \Rightarrow T = 82 + 41 = 123\).
Lời giải
Ta có \(h\left( t \right) = 0 \Leftrightarrow - 0,5{t^2} + 2,75t + 1,5 = 0 \Leftrightarrow t = - 0,5;t = 6\).
\(h\left( t \right) = - 0,5{t^2} + 2,75t + 1,5 = - 0,5{\left( {t - \frac{{11}}{4}} \right)^2} + \frac{{169}}{{32}} \le \frac{{169}}{{32}}\) khi \(t = \frac{{11}}{4} = 2,75\)(giây).
Quả bóng có độ cao lớn hơn \(1,5\) mét so với mặt đất khi:
\(h\left( t \right) > 0 \Leftrightarrow - 0,5{t^2} + 2,75t + 1,5 > 0 \Leftrightarrow - 0,5 < t < 6\)
Mà \(t > 0\) nên suy ra \(0 < t < 6\).
a) Sai: Quả bóng chạm mặt đất khi \(t = 6\) giây.
b) Sai: Quả bóng có độ cao lớn hơn \(1,5\) mét so với mặt đất trong thời gian là \(6\) giây.
c) Đúng: Quả bóng đạt độ cao lớn nhất khi \(t = 2,75\) giây.
d) Đúng: Quả bóng có độ cao lớn hơn \(1,5\) mét so với mặt đất trong khoảng thời gian \(0 < t < 6\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.