(4 điểm)
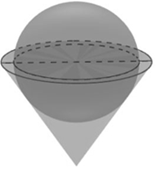
Một bình đựng đầy nước có dạng hình nón (không có đáy). Người ta thả vào đó một khối cầu có đường kính bằng chiều cao của bình nước và đo được thể tích nước tràn ra ngoài là 18π dm3. Biết rằng khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng một nửa của khối cầu đã chìm trong nước (hình dưới đây). Tính thể tích nước còn lại trong bình.

Quảng cáo
Trả lời:
Một bình đựng đầy nước có dạng hình nón (không có
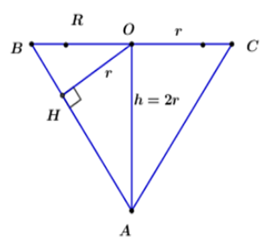
Gọi r là bán kính khối cầu; \(R\) là bán kính khối nón; \(h\) là chiều cao khối nón
Ta có \(h = 2r\) (dm)
Theo đề bài ta có:
Thể tích nửa khối cầu là 18π (dm3)
Suy ra \(r = 3\) (dm) và \(h = 6\) (dm)
Xét tam giác \(OAB\) vuông tại \(O\) có đường cao \(OH\) nên \(R = \frac{{2\sqrt 3 }}{3}r = 2\sqrt 3 \) (dm)
Khi đó thể tích khối nón sẽ là \(24\pi \)(dm3)
Vậy thể tích nước còn lại trong bình là \(6\pi \)(dm3)
Câu hỏi cùng đoạn
Câu 2:
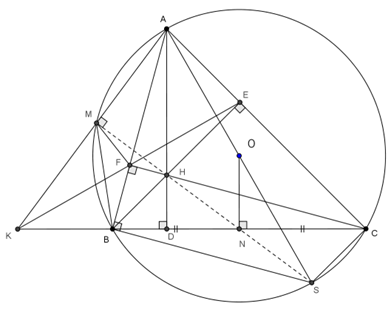
Cho \(\Delta ABC\) nhọn \(\left( {AB < AC} \right)\) nội tiếp đường tròn \(\left( O \right)\). Các đường cao \(AD,{\rm{ }}BE,CF\) cắt nhau tại \(H\). Tia \(EF\) cắt tia \(CB\) tại \(K\).
a) Chứng minh tứ giác \(BFEC\) nội tiếp và \(KE.KF = KB.KC\).
b) Đường thẳng \(KA\) cắt \(\left( O \right)\) tại \(M\). Chứng minh tứ giác \(AEFM\) nội tiếp.
c) Gọi \(N\) là trung điểm \(BC\). Chứng minh \(M,{\rm{ }}H,{\rm{ }}N\) thẳng hàng.
Cho \(\Delta ABC\) nhọn \(\left( {AB < AC} \right)\) nội tiếp đường tròn \(\left( O \right)\). Các đường cao \(AD,{\rm{ }}BE,CF\) cắt nhau tại \(H\). Tia \(EF\) cắt tia \(CB\) tại \(K\).
a) Chứng minh tứ giác \(BFEC\) nội tiếp và \(KE.KF = KB.KC\).
b) Đường thẳng \(KA\) cắt \(\left( O \right)\) tại \(M\). Chứng minh tứ giác \(AEFM\) nội tiếp.
c) Gọi \(N\) là trung điểm \(BC\). Chứng minh \(M,{\rm{ }}H,{\rm{ }}N\) thẳng hàng.
a) Chứng minh \(BFEC\) là tứ giác nội tiếp.
Tứ giác \(BFEC\) có:
\(\widehat {BFC} = \widehat {BEC} = 90^\circ \) (\(BE,{\rm{ }}CF\) là hai đường cao của \(\Delta ABC\))
\( \Rightarrow \) tứ giác \(BFEC\) nội tiếp đường tròn đường kính \(BC\).
Chứng minh \(KE.KF = KB.KC\)
Xét hai tam giác \(\Delta KEB\) và \(\Delta KCF\) có: \(\widehat {EKC}\) là góc chung và \(\widehat {KEB} = \widehat {KCF}\) (hai góc nội tiếp cùng chắn cung )
\(\begin{array}{l} \Rightarrow \Delta KEB{\rm{ }} = {\rm{ }}\Delta KCF{\rm{ }}\left( {g - g} \right)\\ \Rightarrow \frac{{KE}}{{KC}} = \frac{{KB}}{{KF}}\\ \Rightarrow KE.KF = KB.KC{\rm{ }}\left( 1 \right)\end{array}\)
b) Chứng minh \(AEFM\) là tứ giác nội tiếp.
Tứ giác \(AMBC\) nội tiếp (\(A,{\rm{ }}M,{\rm{ }}B,{\rm{ }}C\) thuộc \(\left( O \right)\))
\(\begin{array}{l} \Rightarrow \widehat {KMB} = \widehat {KCA}\\ \Rightarrow \Delta KMB{\rm{ }} = {\rm{ }}\Delta KCA{\rm{ }}\left( {g - g} \right)\\ \Rightarrow KM.KA = KB.KC{\rm{ }}\left( 2 \right)\end{array}\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra
\[\begin{array}{l} \Rightarrow KM.KA = KE.KF\\ \Rightarrow \Delta KMF{\rm{ }} = {\rm{ }}\Delta KEA{\rm{ }}\left( {c - g - c} \right)\\ \Rightarrow \widehat {KMF} = \widehat {KEA}{\rm{ }}\end{array}\]
Suy ra tứ giác \(AEFM\) nội tiếp. \(\left( 3 \right)\)
c)Chứng minh ba điểm \(M,{\rm{ }}H,{\rm{ }}N\) thẳng hàng.
Gọi \(AS\) là đường kính của \(\left( O \right)\)
\( \Rightarrow \widehat {ACS} = {90^0}\) và \(\widehat {ABS} = {90^0}\) (góc nội tiếp chắn nửa đường tròn, \(AS\) là đường kính)
\( \Rightarrow BHCS\) là hình bình hành \( \Rightarrow H,{\rm{ }}N,{\rm{ }}S\) thẳng hàng.
Ta có \(AFHE\) nội tiếp (\(\widehat {AFH} + \widehat {AEH} = {90^0} + {90^0} = {180^0}\)) \(\left( 4 \right)\)
Từ \(\left( 4 \right)\) và \(\left( 4 \right)\) \[ \Rightarrow A,{\rm{ }}M,{\rm{ }}F,{\rm{ }}H,{\rm{ }}E\] cùng thuộc một đường tròn
\( \Rightarrow AMHE\) nội tiếp \( \Rightarrow \widehat {MHA} = {90^0} \Rightarrow HM \bot AK\) tại \(M\)
Ta có \(\widehat {AMS} = {90^0}\) (góc nội tiếp chắn nửa đường tròn, \(AS\) đường kính) \( \Rightarrow SM \bot AK\) tại \(M\)
Tóm lại:
\(H,{\rm{ }}N,{\rm{ }}S\) thẳng hàng (chứng minh trên)
\(HM \bot AK\) tại \(M\)(chứng minh trên)
\(SM \bot AK\) tại \(M\) (chứng minh trên)
\( \Rightarrow S,{\rm{ }}N,{\rm{ }}H,{\rm{ }}M\) thẳng hàng.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi số bước chân anh Sơn và chị Hà đi được trong 1 phút lần lượt là x và y \(\left( {x,y \in {\mathbb{N}^*}} \right).\)
Vì nếu cùng đi trong 2 phút thì anh Sơn bước nhiều hơn chị Hà 20 bước nên ta có phương trình \(2x - 2y = 20\) (1).
Vì nếu chị Hà đi trong 5 phút thì lại nhiều hơn anh Sơn đi trong 3 phút là 160 bước từ đó ta có \(5y - 3x = 160\) (2).
Từ (1) và (2) suy ra x = 105 và y = 95.
Vậy trong một giờ anh Sơn đi được \(105.60 = 6300\)
trong một giờ chị Hà đi được \(95.60 = 5700\).
Do anh Sơn và chị Hà đề ra mục tiêu mỗi ngày một người phải đi bộ ít nhất 6000 bước nên anh Sơn đã đạt được mục tiêu tối thiểu mà mình đề ra, còn chị Hà thì chưa.
Lời giải
Từ bảng tần số trên ta thấy có \(12\) học viên đạt điểm từ \(\left[ {7,5;10} \right)\).
Vậy có 12 học viên xếp loại \(A\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.