(1,5 điểm)
Biểu đồ cột kép ở Hình \[30\] biểu diễn số lượng học sinh tham gia giải thi đấu thể thao của một trường trung học cơ sơ.
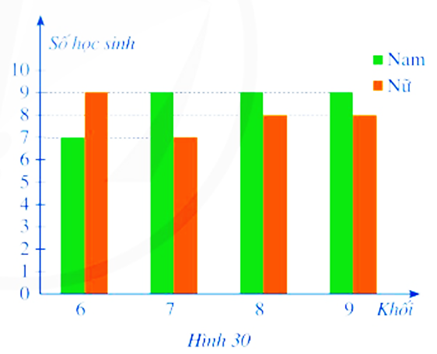
Chọn ngẫu nhiên một học sinh tham gia giải thi đấu thể thao của trường đó. Tính xác suất của mỗi biến cố sau:
A: “Học sinh được chọn là nam”;
B: “Học sinh được chọn thuộc khối \[6\]”;
C: “Học sinh được là nữ và không thuộc khối \[9\]”.
Biểu đồ cột kép ở Hình \[30\] biểu diễn số lượng học sinh tham gia giải thi đấu thể thao của một trường trung học cơ sơ.
Chọn ngẫu nhiên một học sinh tham gia giải thi đấu thể thao của trường đó. Tính xác suất của mỗi biến cố sau:
A: “Học sinh được chọn là nam”;
B: “Học sinh được chọn thuộc khối \[6\]”;
C: “Học sinh được là nữ và không thuộc khối \[9\]”.
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 22 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Nhìn vào biểu đồ ta thấy:
- Lớp \[6\] có tất cả: \[7\]nam +\[\;9\] nữ = \[16\] học sinh
- Lớp \[7\] có tất cả: \[9\]nam + \[7\] nữ = \[16\]học sinh
- Lớp \[8\] có tất cả: \[9\]nam + \[8\] nữ = \[17\] học sinh
- Lớp \[9\]có tất cả: \[9\]nam + \[8\] nữ = \[17\] học sinh
Như vậy, không gian mẫu trong bài này có tất cả \[16 + 16 + 17 + 17 = 66\] học sinh.
- Số kết quả thuận lợi cho biến cố \[A\] là: \[7 + 9 + 9 + 9 = 34\] học sinh
Xác suất để biến cố \[A\]xảy ra là: \(P\left( A \right) = \frac{{34}}{{66}} = \frac{{17}}{{33}}\)
- Số kết quả thuận lợi cho biến cố \[B\]là: \[16\]học sinh
Xác suất để biến cố \[B\] xảy ra là: \(P\left( B \right) = \frac{{16}}{{66}} = \frac{8}{{33}}\)
- Số kết quả thuận lợi cho biến cố \[C\] là: \[9 + 7 + 8 = 24\] học sinh
Xác suất để biến cố \[C\] xảy ra là: \(P\left( C \right) = \frac{{24}}{{66}} = \frac{{12}}{{33}}\).
Câu hỏi cùng đoạn
Câu 2:
Một hộp đựng \[5\] tấm thẻ ghi các số \[1\];\[2\];\[3\];\[4\];\[5\]Rút ngẫu nhiên lần lượt hai tấm thẻ từ hộp, tấm thẻ rút ra lần đầu không trả lại vào hộp.
a) Phép thử và kết quả của phép thử là gì?
b) Mô tả không gian mẫu của phép thử. Không gian mẫu có bao nhiêu phần tử?
Một hộp đựng \[5\] tấm thẻ ghi các số \[1\];\[2\];\[3\];\[4\];\[5\]Rút ngẫu nhiên lần lượt hai tấm thẻ từ hộp, tấm thẻ rút ra lần đầu không trả lại vào hộp.
a) Phép thử và kết quả của phép thử là gì?
b) Mô tả không gian mẫu của phép thử. Không gian mẫu có bao nhiêu phần tử?
Giải bởi Vietjack
a) Phép thử: Rút ngẫu nhiên lần lượt hai tấm thẻ từ hộp, tấm thẻ rút ra lần đầu không trả lại vào hộp.
Kết quả của phép thử:
- Lần rút thứ nhất:\[5\] kết quả có thể xảy ra (\[1\];\[2\];\[3\];\[4\];\[5\] )
- Lần rút thứ hai: \[4\] kết quả có thể xảy ra (vì sau lần rút thứ nhất, chit còn lại \[4\] thẻ trong hộp).
b)Mô tả không gian mẫu của phép thử:
Liệt kê tất cả các kết quả có thể xảy ra của phép thử. Sử dụng cặp số \[\left( {x,y} \right)\] để mô tả kết quả với:
- \[x\]là số trên thẻ rút ra lần thứ nhất.
- \[y\]là số trên thẻ rút ra lần thứ hai.
|
Lần 2 Lần 1 |
1 |
2 |
3 |
4 |
5 |
|
1 |
\[\left( {1;1} \right)\] |
\[\left( {1;2} \right)\] |
\[\left( {1;3} \right)\] |
\[\left( {1;4} \right)\] |
\[(1;5)\] |
|
2 |
\[\left( {2;1} \right)\] |
\[\left( {2;2} \right)\] |
\[\left( {2;3} \right)\] |
\[\left( {2;4} \right)\] |
\[\left( {2;5} \right)\] |
|
3 |
\[\left( {3;1} \right)\] |
\[\left( {3;2} \right)\] |
\[\left( {3;3} \right)\] |
\[\left( {3;4} \right)\] |
\[\left( {3;5} \right)\] |
|
4 |
\[\left( {4;1} \right)\] |
\[\left( {4;2} \right)\] |
\[\left( {4;{\rm{ }}3} \right)\] |
\[\left( {4;4} \right)\] |
\[\left( {4;5} \right)\] |
|
5 |
\[\left( {5,1} \right)\] |
\[\left( {5,2} \right)\] |
\[\left( {5;3} \right)\] |
\[\left( {5;4} \right)\] |
\[\left( {5;5} \right)\] |
Vì tấm thẻ rút ra lần đầu không trả lại vào hộp.
Không gian mẫu:
\(\Omega = \left\{ \begin{array}{l}\left( {1;2} \right)\,;\left( {1;3} \right);\left( {1;4} \right);\left( {1;5} \right);\left( {2;1} \right);\left( {2;3} \right);\left( {2;4} \right);\left( {2;5} \right);\left( {3;1} \right);\left( {3;2} \right);\left( {3;4} \right);\left( {3;5} \right);\left( {4;1} \right);\left( {4;2} \right);\\\left( {4;3} \right);\left( {4;5} \right);\left( {5;1} \right);\left( {5;2} \right);\left( {5;3} \right);\left( {5;4} \right)\end{array} \right\}\)
Vậy không gian mẫu có \[20\] phần tử.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
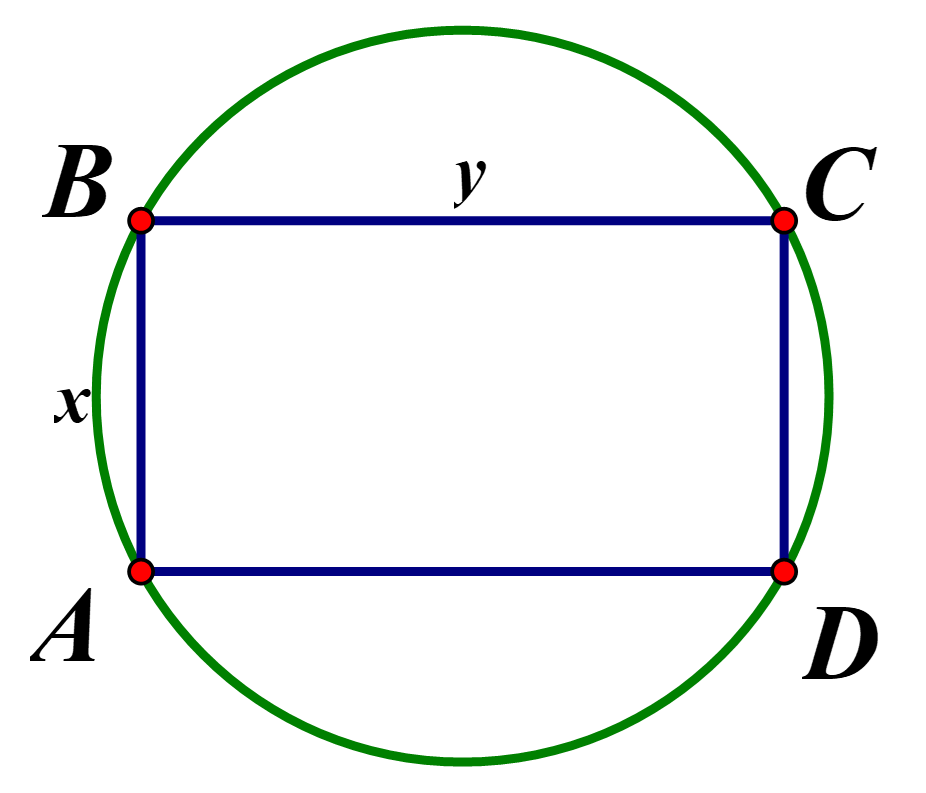
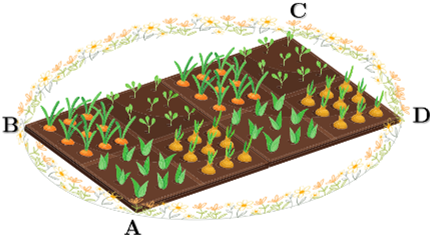
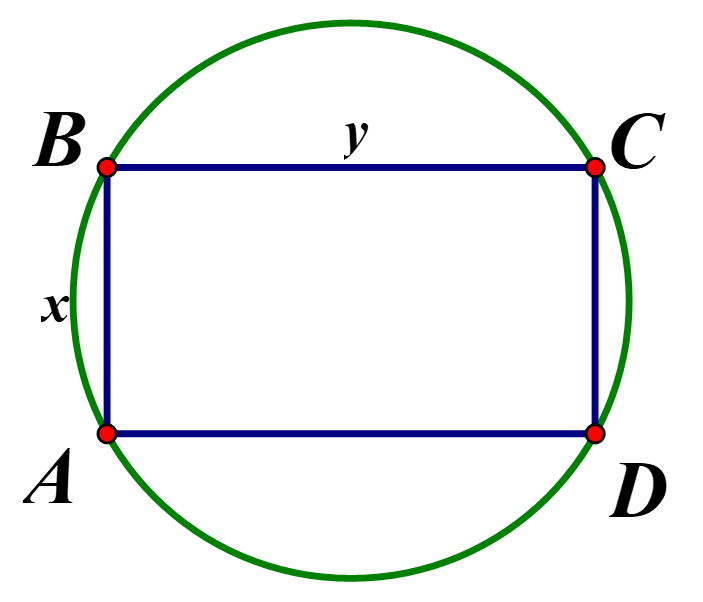
Độ dài đường kính của đường tròn là đường chéo của hình chữ nhật \(ABCD\),
Vậy biểu thức xác định đường kính của đường tròn là \(\sqrt {{x^2} + {y^2}} \)
Vậy bán kính của đường tròn là \(\frac{{\sqrt {{x^2} + {y^2}} }}{2}\)
Diện tích đường tròn là \(S = \pi .\frac{{{x^2} + {y^2}}}{4}\)
Diện tích của hình chữ nhật là \({S_{hcn}} = xy = 640\left( {{m^2}} \right)\)
Diện tích phần đất trồng hoa là
\(S' = S - {S_{hcn}} = \pi .\frac{{{x^2} + {y^2}}}{4} - xy\;\)
Có \({\left( {x - y} \right)^2} \ge 0\) với mọi \(x;y\)
\[ \Rightarrow \]\({x^2} - 2xy + {y^2} \ge 0\)\[ \Rightarrow \]\({x^2} + {y^2} \ge 2xy\)\[ \Rightarrow \]\(\frac{{{x^2} + {y^2}}}{4} \ge \frac{{xy}}{2} > 0\)
\[ \Rightarrow \]\(\frac{{\pi \left( {{x^2} + {y^2}} \right)}}{4} \ge \frac{{\pi xy}}{2}\)\[ \Rightarrow \]\(\frac{{\pi \left( {{x^2} + {y^2}} \right)}}{4} - xy \ge \frac{{\pi xy}}{2} - xy\)
Vậy \(S' \ge \frac{{\pi xy}}{2} - xy\;\)\[ \Rightarrow \]\(S \ge 320\pi - 640\)
Vậy để diện tích của bốn phần đất trồng hoa nhỏ nhất thì \(x = y\)
Khi đó \(x = y = 8\sqrt {10} \) (m)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đổi \(80\,{\rm{mm}}\, = \,8\,{\rm{cm}}\)
Phần thể tích nước dâng lên chính là thể tích của phần đá chìm trong nước của cục đá đó.
Nên thể tích phần đá chìm trong nước của cục đá đó là: \(16,5\,.\,8 = 132\,{\rm{c}}{{\rm{m}}^3}\)Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập