Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 22

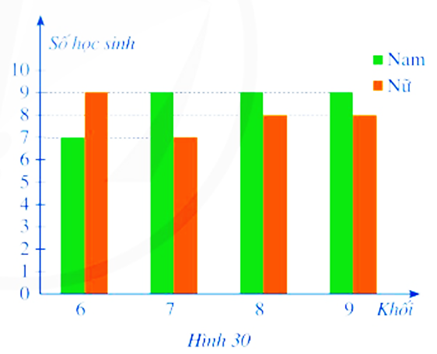
Nhìn vào biểu đồ ta thấy:

- Lớp \[6\] có tất cả: \[7\]nam +\[\;9\] nữ = \[16\] học sinh

- Lớp \[7\] có tất cả: \[9\]nam + \[7\] nữ = \[16\]học sinh

- Lớp \[8\] có tất cả: \[9\]nam + \[8\] nữ = \[17\] học sinh

- Lớp \[9\]có tất cả: \[9\]nam + \[8\] nữ = \[17\] học sinh

Như vậy, không gian mẫu trong bài này có tất cả \[16 + 16 + 17 + 17 = 66\] học sinh.

- Số kết quả thuận lợi cho biến cố \[A\] là: \[7 + 9 + 9 + 9 = 34\] học sinh

Xác suất để biến cố \[A\]xảy ra là: \(P\left( A \right) = \frac{{34}}{{66}} = \frac{{17}}{{33}}\) 

- Số kết quả thuận lợi cho biến cố \[B\]là: \[16\]học sinh

Xác suất để biến cố \[B\] xảy ra là: \(P\left( B \right) = \frac{{16}}{{66}} = \frac{8}{{33}}\) 

- Số kết quả thuận lợi cho biến cố \[C\] là: \[9 + 7 + 8 = 24\] học sinh

Xác suất để biến cố \[C\] xảy ra là: \(P\left( C \right) = \frac{{24}}{{66}} = \frac{{12}}{{33}}\).

1) Tính giá trị của \(A\) khi \(x = 25\)

Biểu thức: \(A = \frac{{\sqrt x  + 3}}{{\sqrt x  + 1}}\)

Điều kiện: \(x \ge 0\)

Với \(x = 25\) thỏa mãn điều kiện

Thay \(x = 25\) vào biểu thức \(A\) ta có: \(A = \frac{{\sqrt {25}  + 3}}{{\sqrt {25}  + 1}} = \frac{8}{6} = \frac{4}{3}\)

Vậy với \(x = 25\) thì \(A = \frac{4}{3}\)

2) Rút gọn \(B\)

Điều kiện xác định: \(x \ge 0\); \(x \ne 4\); \( \ne x \ne 9\)

Ta có: \(B = \frac{{\sqrt x }}{{\sqrt x  - 2}} - \frac{{\sqrt x  + 2}}{{3 - \sqrt x }} - \frac{{x - 3\sqrt x  + 5}}{{x - 5\sqrt x  + 6}}\)

\(B = \frac{{\sqrt x }}{{\sqrt x  - 2}} + \frac{{\sqrt x  + 2}}{{\sqrt x  - 3}} - \frac{{x - 3\sqrt x  + 5}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}}\)

\(B = \frac{{\sqrt x \left( {\sqrt x  - 3} \right) + \left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right) - \left( {x - 3\sqrt x  + 5} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}}\)

\(B = \frac{{x - 3\sqrt x  + x - 4 - x + 3\sqrt x  - 5}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}}\)

\(B = \frac{{x - 9}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}}\)

\(B = \frac{{\left( {\sqrt x  + 3} \right)\left( {\sqrt x  - 3} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}}\)

\(B = \frac{{\sqrt x  + 3}}{{\sqrt x  - 2}}\)

Vậy \(B = \frac{{\sqrt x  + 3}}{{\sqrt x  - 2}}\)

3) Cho \(P = A:B\). Tìm \(x\) để \(2P = 2\sqrt x  - 9\)

Điều kiện xác định: \(x \ge 0\); \(x \ne 4\); \( \ne x \ne 9\)

Ta có: \(P = A:B\)\( = \frac{{\sqrt x  + 3}}{{\sqrt x  + 1}}:\frac{{\sqrt x  + 3}}{{\sqrt x  - 2}}\)\( = \frac{{\sqrt x  + 3}}{{\sqrt x  + 1}}.\frac{{\sqrt x  - 2}}{{\sqrt x  + 3}}\)\( = \frac{{\sqrt x  - 2}}{{\sqrt x  + 1}}\)

Để \(2P = 2\sqrt x  - 9\)

\(\frac{{2\left( {\sqrt x  - 2} \right)}}{{\sqrt x  + 1}} = 2\sqrt x  - 9\)

\(2\sqrt x  - 4 = \left( {2\sqrt x  - 9} \right)\left( {\sqrt x  + 1} \right)\)

\(2\sqrt x  - 4 = 2x + 2\sqrt x  - 9\sqrt x  - 9\)

\(2x - 9\sqrt x  + 5 = 0\)

\(\left( {2\sqrt x  + 1} \right)\left( {\sqrt x  - 5} \right) = 0\)

\(\left[ \begin{array}{l}2\sqrt x  + 1 = 0\,\,{\rm{(PTVN)}}\\\sqrt x  - 5 = 0\end{array} \right.\)

\(\sqrt x  - 5 = 0\)

\(x = 25\) (TM)

Vậy để \(2P = 2\sqrt x  - 9\) thì \(x = 25\).

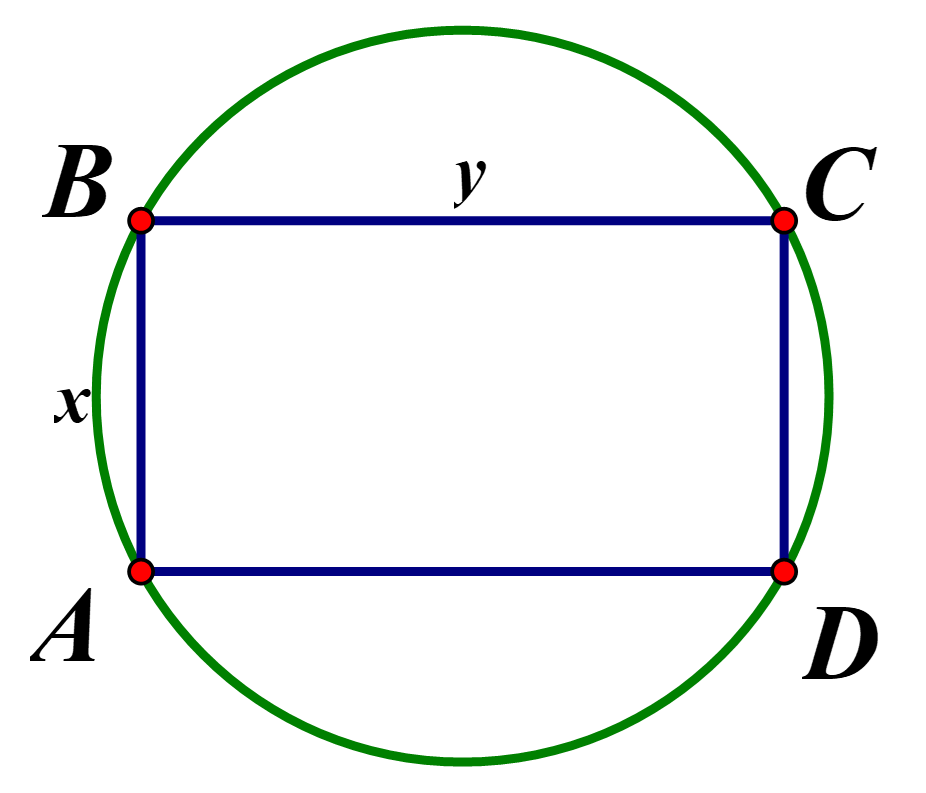
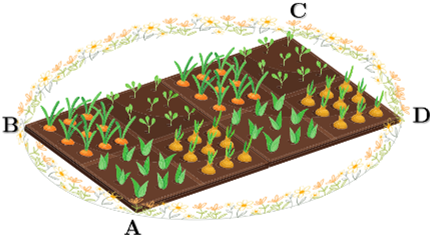
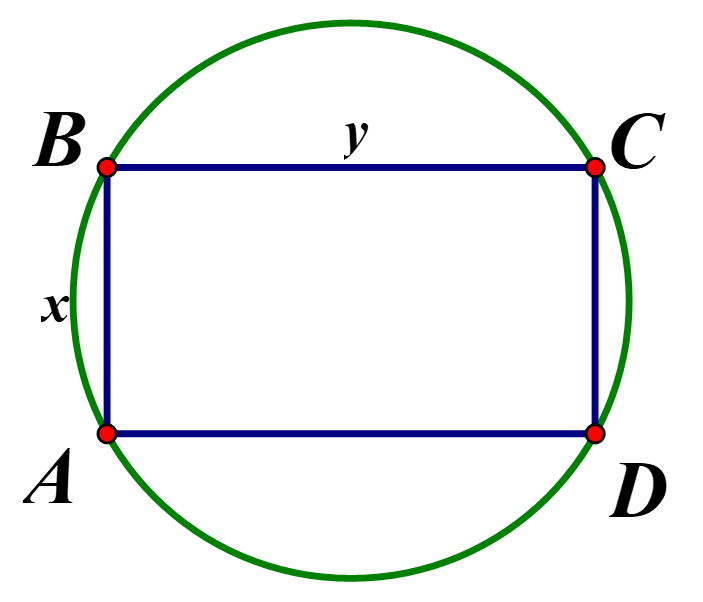
Độ dài đường kính của đường tròn là đường chéo của hình chữ nhật \(ABCD\),

Vậy biểu thức xác định đường kính của đường tròn là  \(\sqrt {{x^2} + {y^2}} \)

Vậy bán kính của đường tròn là \(\frac{{\sqrt {{x^2} + {y^2}} }}{2}\)

Diện tích đường tròn là \(S = \pi .\frac{{{x^2} + {y^2}}}{4}\)

Diện tích của hình chữ nhật là \({S_{hcn}} = xy = 640\left( {{m^2}} \right)\)

Diện tích phần đất trồng hoa là

                           \(S' = S - {S_{hcn}} = \pi .\frac{{{x^2} + {y^2}}}{4} - xy\;\)

Có \({\left( {x - y} \right)^2} \ge 0\) với mọi \(x;y\)

\[ \Rightarrow \]\({x^2} - 2xy + {y^2} \ge 0\)\[ \Rightarrow \]\({x^2} + {y^2} \ge 2xy\)\[ \Rightarrow \]\(\frac{{{x^2} + {y^2}}}{4} \ge \frac{{xy}}{2} > 0\)

\[ \Rightarrow \]\(\frac{{\pi \left( {{x^2} + {y^2}} \right)}}{4} \ge \frac{{\pi xy}}{2}\)\[ \Rightarrow \]\(\frac{{\pi \left( {{x^2} + {y^2}} \right)}}{4} - xy \ge \frac{{\pi xy}}{2} - xy\)

Vậy \(S' \ge \frac{{\pi xy}}{2} - xy\;\)\[ \Rightarrow \]\(S \ge 320\pi  - 640\)

Vậy để diện tích của bốn phần đất trồng hoa nhỏ nhất thì \(x = y\)

Khi đó \(x = y = 8\sqrt {10} \) (m)

Gọi số sản phẩm tháng thứ nhất đội \[I\] làm được là \[x\] (sản phẩm) \(\left( {x \in {\mathbb{N}^*},x < 1100} \right)\)

Số sản phẩm tháng thứ nhất đội \[II\] làm được là \[y\] (sản phẩm) \(\left( {y \in {\mathbb{N}^*},y < 1100} \right)\)

Vì tháng thứ nhất hai đội sản xuất được \(1100\) sản phẩm nên ta có phương trình

\(x + y = 1100\)  \(\left( 1 \right)\)

Số sản phẩm tháng thứ hai đội \[I\] làm được là \[x + 15\% x = 1,15x\] (sản phẩm)

Số sản phẩm tháng thứ hai đội \[II\] làm được là \[y + 20\% y = 1,2y\] (sản phẩm)

Theo bài ra ta có phương trình \[1,15x + 1,2y = 1295\]   \[\left( 2 \right)\]

Từ  \(\left( 1 \right)\) và \[\left( 2 \right)\] ta có hệ phương trình \(\left\{ \begin{array}{l}x + y = 1100\\1,15x + 1,2y = 1295\end{array} \right.\)

\(\left\{ \begin{array}{l}1,15x + 1,15y = 1265\\1,15x + 1,2y = 1295\end{array} \right.\)                     \(\left\{ \begin{array}{l}0,05y = 30\\x + y = 1100\end{array} \right.\)                    \(\left\{ \begin{array}{l}y = 600\\x + y = 1100\end{array} \right.\)

\(\left\{ \begin{array}{l}y = 600\\x + 600 = 1100\end{array} \right.\)                       \(\left\{ \begin{array}{l}y = 600\\x = 500\end{array} \right.\) (thoả mãn điều kiện)

Vậy tháng thứ nhất đội \[I\] làm được là \[500\] (sản phẩm), đội \[II\] làm được là \[600\] (sản