(2,5 điểm)
Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Tháng thứ nhất hai đội sản xuất được \(1100\) sản phẩm. Sang tháng thứ hai, đội \(I\) làm vượt mức \(15\% \) và đội \(II\) làm vượt mức \(20\% \) so với tháng thứ nhất, vì vậy cả hai đội đã làm được \(1295\) sản phẩm. Hỏi trong tháng thứ nhất mỗi đội làm được bao nhiêu sản phẩm ?
Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Tháng thứ nhất hai đội sản xuất được \(1100\) sản phẩm. Sang tháng thứ hai, đội \(I\) làm vượt mức \(15\% \) và đội \(II\) làm vượt mức \(20\% \) so với tháng thứ nhất, vì vậy cả hai đội đã làm được \(1295\) sản phẩm. Hỏi trong tháng thứ nhất mỗi đội làm được bao nhiêu sản phẩm ?
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 22 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi số sản phẩm tháng thứ nhất đội \[I\] làm được là \[x\] (sản phẩm) \(\left( {x \in {\mathbb{N}^*},x < 1100} \right)\)
Số sản phẩm tháng thứ nhất đội \[II\] làm được là \[y\] (sản phẩm) \(\left( {y \in {\mathbb{N}^*},y < 1100} \right)\)
Vì tháng thứ nhất hai đội sản xuất được \(1100\) sản phẩm nên ta có phương trình
\(x + y = 1100\) \(\left( 1 \right)\)
Số sản phẩm tháng thứ hai đội \[I\] làm được là \[x + 15\% x = 1,15x\] (sản phẩm)
Số sản phẩm tháng thứ hai đội \[II\] làm được là \[y + 20\% y = 1,2y\] (sản phẩm)
Theo bài ra ta có phương trình \[1,15x + 1,2y = 1295\] \[\left( 2 \right)\]
Từ \(\left( 1 \right)\) và \[\left( 2 \right)\] ta có hệ phương trình \(\left\{ \begin{array}{l}x + y = 1100\\1,15x + 1,2y = 1295\end{array} \right.\)
\(\left\{ \begin{array}{l}1,15x + 1,15y = 1265\\1,15x + 1,2y = 1295\end{array} \right.\) \(\left\{ \begin{array}{l}0,05y = 30\\x + y = 1100\end{array} \right.\) \(\left\{ \begin{array}{l}y = 600\\x + y = 1100\end{array} \right.\)
\(\left\{ \begin{array}{l}y = 600\\x + 600 = 1100\end{array} \right.\) \(\left\{ \begin{array}{l}y = 600\\x = 500\end{array} \right.\) (thoả mãn điều kiện)
Vậy tháng thứ nhất đội \[I\] làm được là \[500\] (sản phẩm), đội \[II\] làm được là \[600\] (sản
Câu hỏi cùng đoạn
Câu 2:
Một cơ sở sản xuất lập kế hoạch làm \(180\) sản phẩm trong một thời gian nhất định. Do cải tiến kĩ thuật, năng suất mỗi ngày tăng \(3\) sản phẩm, vì thế không những hoàn thành sớm một ngày, mà còn vượt mức \(18\) sản phẩm. Hỏi theo kế hoạch mỗi ngày phải sản xuất bao nhiêu sản phẩm?
Một cơ sở sản xuất lập kế hoạch làm \(180\) sản phẩm trong một thời gian nhất định. Do cải tiến kĩ thuật, năng suất mỗi ngày tăng \(3\) sản phẩm, vì thế không những hoàn thành sớm một ngày, mà còn vượt mức \(18\) sản phẩm. Hỏi theo kế hoạch mỗi ngày phải sản xuất bao nhiêu sản phẩm?
Giải bởi Vietjack
Gọi số sản phẩm theo kế hoạch cơ sở cần sản xuất trong một ngày là: \(x\) (sản phẩm, \(x > 0\))
Số sản phẩm thực tế cơ sở cần sản xuất trong một ngày là: \(x + 3\) (sản phẩm, \(x > 0\))
Sản phẩm cơ sở cần hoàn thành theo kế hoạch là: \(180\) (sản phẩm)
Thực tế cơ sở sản xuất vượt mức \(18\) sản phẩm theo kế hoạch
Số sản phẩm thực tế là: \(198\) (sản phẩm)
Thời gian theo kế hoạch cơ sở hoàn thành công việc là: \(\frac{{180}}{x}\) (ngày)
Thời gian thực tế cơ sở hoàn thành công việc là: \(\frac{{198}}{{x + 3}}\) (ngày)
Theo bài ra ta có phương trình:
\(\frac{{180}}{x} - \frac{{198}}{{x + 3}} = 1\)
\(180\left( {x + 3} \right) - 198x = x\left( {x + 3} \right)\)
\(180x + 540 - 198x = {x^2} + 3x\)
\({x^2} + 21x - 540 = 0\)
\[\left[ \begin{array}{l}x = 15\,\,\,\,\,\,\left( {{\rm{TM}}} \right)\\x = - 36\,\,\,\left( {{\rm{KTM}}} \right)\end{array} \right.\]
Vậy theo kế hoạch, mỗi ngày cơ sở cần phải làm \(15\) (sản phẩm)
Câu 3:
Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình : \(\left( * \right)\). Tính giá trị của biểu thức \( \Leftrightarrow \Delta ' > 0 \Leftrightarrow 4 - m > 0 \Leftrightarrow m < 4\)
Giải bởi Vietjack
\({x^2} - 4x - 7 = 0\)
Phương trình có \(ac = - 7 < 0\)nên luôn có 2 nghiệm phân biệt \({x_1},{x_2}\)
Áp dụng hệ thức Vi et ta có : \({x_1} + {x_2} = 4;{x_1}{x_2} = - 7\).
Khi đó ta có :\(T = \frac{{{x_1}}}{{{x_2}}} + \frac{{{x_2}}}{{{x_1}}} - 2 = \frac{{x_1^2 + x_2^2}}{{{x_1}{x_2}}} - 2 = \frac{{{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2}}}{{{x_1}{x_2}}} - 2 = \frac{{{4^2} - 2.\left( { - 7} \right)}}{{ - 7}} - 2 = \frac{{ - 44}}{7}\)
Vậy \(T = - \frac{{44}}{7}\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
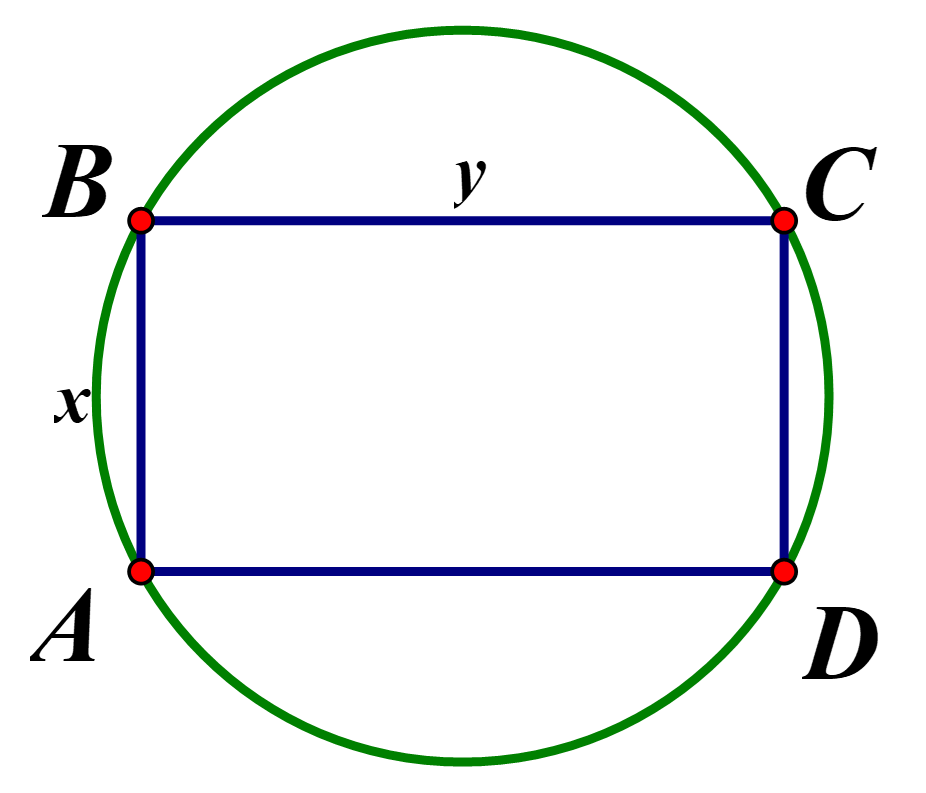
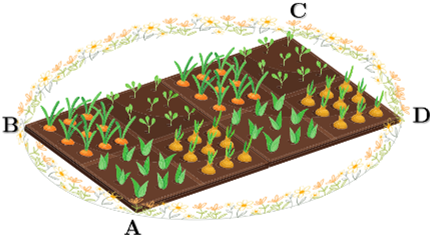
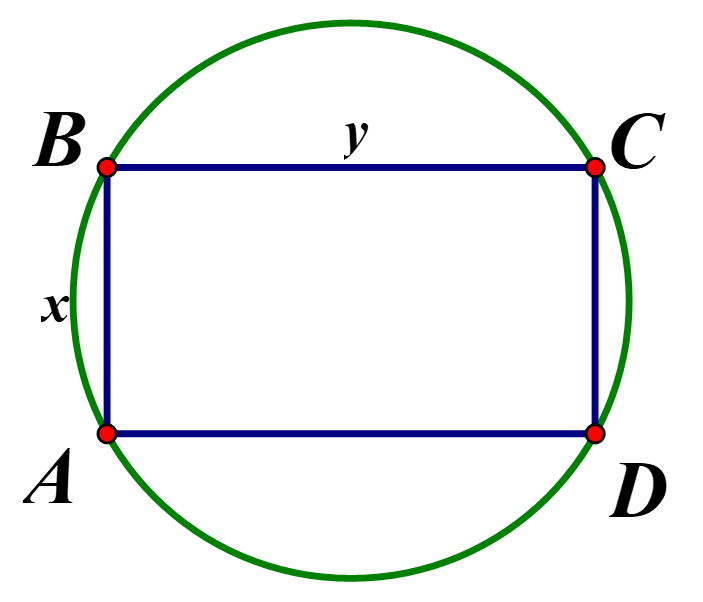
Độ dài đường kính của đường tròn là đường chéo của hình chữ nhật \(ABCD\),
Vậy biểu thức xác định đường kính của đường tròn là \(\sqrt {{x^2} + {y^2}} \)
Vậy bán kính của đường tròn là \(\frac{{\sqrt {{x^2} + {y^2}} }}{2}\)
Diện tích đường tròn là \(S = \pi .\frac{{{x^2} + {y^2}}}{4}\)
Diện tích của hình chữ nhật là \({S_{hcn}} = xy = 640\left( {{m^2}} \right)\)
Diện tích phần đất trồng hoa là
\(S' = S - {S_{hcn}} = \pi .\frac{{{x^2} + {y^2}}}{4} - xy\;\)
Có \({\left( {x - y} \right)^2} \ge 0\) với mọi \(x;y\)
\[ \Rightarrow \]\({x^2} - 2xy + {y^2} \ge 0\)\[ \Rightarrow \]\({x^2} + {y^2} \ge 2xy\)\[ \Rightarrow \]\(\frac{{{x^2} + {y^2}}}{4} \ge \frac{{xy}}{2} > 0\)
\[ \Rightarrow \]\(\frac{{\pi \left( {{x^2} + {y^2}} \right)}}{4} \ge \frac{{\pi xy}}{2}\)\[ \Rightarrow \]\(\frac{{\pi \left( {{x^2} + {y^2}} \right)}}{4} - xy \ge \frac{{\pi xy}}{2} - xy\)
Vậy \(S' \ge \frac{{\pi xy}}{2} - xy\;\)\[ \Rightarrow \]\(S \ge 320\pi - 640\)
Vậy để diện tích của bốn phần đất trồng hoa nhỏ nhất thì \(x = y\)
Khi đó \(x = y = 8\sqrt {10} \) (m)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đổi \(80\,{\rm{mm}}\, = \,8\,{\rm{cm}}\)
Phần thể tích nước dâng lên chính là thể tích của phần đá chìm trong nước của cục đá đó.
Nên thể tích phần đá chìm trong nước của cục đá đó là: \(16,5\,.\,8 = 132\,{\rm{c}}{{\rm{m}}^3}\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập