(0,5 điểm)
Một bồn hình trụ đang chứa dầu, được đặt nằm ngang, có chiều dài bồn là \[5\,m\], có bán kính đáy \[1\,m\], với nắp bồn đặt trên mặt nằm ngang của mặt trụ. Người ta đã rút dầu trong bồn tương ứng với \[0,5\,m\] của đường kính đáy. Tính thể tích gần dầu còn lại trong bồn (kết quả làm tròn 3 chữ số thập phân).
(0,5 điểm)
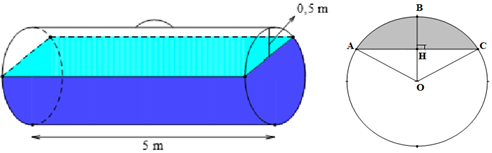
Một bồn hình trụ đang chứa dầu, được đặt nằm ngang, có chiều dài bồn là \[5\,m\], có bán kính đáy \[1\,m\], với nắp bồn đặt trên mặt nằm ngang của mặt trụ. Người ta đã rút dầu trong bồn tương ứng với \[0,5\,m\] của đường kính đáy. Tính thể tích gần dầu còn lại trong bồn (kết quả làm tròn 3 chữ số thập phân).
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 46 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có: \[OH = OB--BH\; = 1--0,5 = 0,5\] (m).
Lại có \[\cos \widehat {AOH} = \frac{{OH}}{{OA}} = \frac{{0,5}}{1} = \frac{1}{2}\]. Suy ra \[\widehat {AOH} = {60^0}\]. Suy ra \[\widehat {AOC} = {120^0}\].
Lại có \[AH = OA.\sin \widehat {AOH} = 1.\sin {60^0} = \frac{{\sqrt 3 }}{2}\]. Suy ra \[AC = 2AH = \sqrt 3 \] (m).
Diện tích hình quạt \(OAC\) là \({S_1} = \frac{{\pi .{R^2}.n}}{{360}} = \frac{{\pi {{.1}^2}.120}}{{360}} = \frac{\pi }{3}\) (\({m^2}\))
Diện tích tam giác \(OAC\) là \({S_2} = \frac{1}{2}.OH.AC = \frac{1}{2}.0,5.\sqrt 3 = \frac{{\sqrt 3 }}{4}\) (\({m^2}\)).
Diện tích hình viên phân (diện tích màu tô đậm) là \[S = \frac{\pi }{3} - \frac{{\sqrt 3 }}{4} = \frac{{4\pi - 3\sqrt 3 }}{{12}}\] (\({m^2}\)).
Thể tích bồn dầu ban đầu là \({V_1} = \pi {R^2}h = \pi {.1^2}.5 = 5\pi \,\,({m^3})\).
Thể tích phần dầu đã lấy ra là \({V_2} = 5.S = \frac{{5\left( {4\pi - 3\sqrt 3 } \right)}}{{12}}\) (\({m^3}\)).
Thể tích dầu còn lại trong bồn chứa là \[V = {V_1} - {V_2} = 5\pi - \frac{{5\left( {4\pi - 3\sqrt 3 } \right)}}{{12}} \approx 12,637\].
Vậy bồn còn khoảng 12,637 m3 xăng.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi chiều dài, chiều rộng của mảnh đất hình chữ nhật lần lượt là \(x \left( m \right)\), \(y \left( m \right)\).
Điều kiện: \(x > y > 0\)
Vì chu vi của mảnh đất là \(120 m\) nên \(2\left( {x + y} \right) = 120 \Leftrightarrow x + y = 60\) \(\left( 1 \right)\)
Diện tích của mảnh dất ban đầu là \(xy \left( {{m^2}} \right)\)
Nếu tăng chiều dài thêm \(5\,m\) và tăng chiều rộng thêm \(3\,m\) thì chiều dài mảnh đất là \(x + 5 \left( m \right)\) và
chiều rộng mảnh đất là \(y + 3 \left( m \right)\). Khi đó diện tích mảnh đất tăng thêm \(245\,{m^2}\) nên
\(\left( {x + 5} \right)\left( {y + 3} \right) - xy = 245 \Rightarrow 5x + 3y = 260\) \(\left( 2 \right)\)
Từ \(\left( 1 \right), \left( 2 \right)\) ta có hệ phương trình \(\left\{ \begin{array}{l}x + y = 60\\5x + 3y = 260\end{array} \right.\)
Giải hệ phương trình, ta được: \(\left\{ \begin{array}{l}x = 40\\y = 20\end{array} \right.\) ( thỏa mãn)
Vậy chiều dài và chiều rộng của mảnh đất đó là \(40\,m\) và \(20\,m\)
Lời giải
a). Diện tích inox để làm nên chiếc xô hình trụ trên là:
S = Sxung quanh + Sđáy \( \approx 2.\pi .0,2.0,6 + {0,2^2}.\pi = 0,28.\pi \left( {{m^2}} \right)\).
Vậy diện tích inox để làm nên chiếc xô hình trụ trên \[0,28\pi \,{m^2}\]
b). Thể tích nước có trong xô là
\(V = \pi .{R^2}.\frac{2}{3}h = \pi {.0,2^2}.\frac{2}{3}0,6 = 0,016.\pi ({m^3})\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập