Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 46

Có tất cả: \[1 + 5 + 9 + 5 = 20\] học sinh tham gia

                 Bảng tần số tương đối ghép nhóm cho kết quả trên là:

Không gian mẫu của phép thử là \[\Omega  = \left\{ {2;3;...;29;30} \right\}\]. \[\Omega \] có \(29\)phần tử.

                Các kết quả của phép thử là đồng khả năng.

               + Có 10 kết quả thuận lợi cho biến cố A là:\[2;{\rm{ }}3;{\rm{ }}5;{\rm{ }}7;{\rm{ }}11;{\rm{ }}13;{\rm{ }}17;{\rm{ }}19;{\rm{ }}23;{\rm{ }}29\].  

                                  Xác suất của biến cố A là \[P\left( A \right) = \frac{{10}}{{29}}\].

1). Thay\(x = 16\) (TMĐK) vào biểu thức \(A\) ta được \(A = \frac{3}{4}\)  và kết luận.           

2). \(B = \)\(\frac{{\sqrt x \left( {\sqrt x  + 2} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}} + \frac{{\sqrt x  - 1}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}} - \frac{{3\sqrt x }}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}}\)

         \( = \frac{{x + 2\sqrt x  + \sqrt x  - 1 - 3\sqrt x }}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}} = \frac{{x - 1}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}}\)

         \( = \frac{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}}\)

         \( = \frac{{\sqrt x  + 1}}{{\sqrt x  + 2}}\)         

                   3). Với \(x \ge 0,x \ne 1\)

      \(P = A.B\)\( = \frac{{\sqrt x  + 3}}{{\sqrt x  + 1}}.\frac{{\sqrt x  + 1}}{{\sqrt x  + 2}} = \frac{{\sqrt x  + 3}}{{\sqrt x  + 2}} = 1 + \frac{1}{{\sqrt x  + 2}}\)

                           Vì \(\sqrt x  \ge 0,\forall x \ge 0\) nên \(\sqrt x  + 2 > 0\)
            \( \Rightarrow \frac{1}{{\sqrt x  + 2}} > 0 \Rightarrow P > 1 \Rightarrow \sqrt P  > 1\)\( \Rightarrow P - \sqrt P  = \sqrt P (\sqrt P  - 1) > 0 \Rightarrow P > \sqrt P \)

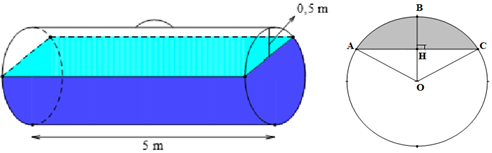
Ta có: \[OH = OB--BH\; = 1--0,5 = 0,5\] (m).

Lại có \[\cos \widehat {AOH} = \frac{{OH}}{{OA}} = \frac{{0,5}}{1} = \frac{1}{2}\]. Suy ra \[\widehat {AOH} = {60^0}\]. Suy ra \[\widehat {AOC} = {120^0}\].

Lại có \[AH = OA.\sin \widehat {AOH} = 1.\sin {60^0} = \frac{{\sqrt 3 }}{2}\]. Suy ra \[AC = 2AH = \sqrt 3 \] (m).

Diện tích hình quạt \(OAC\) là \({S_1} = \frac{{\pi .{R^2}.n}}{{360}} = \frac{{\pi {{.1}^2}.120}}{{360}} = \frac{\pi }{3}\) (\({m^2}\))

Diện tích tam giác \(OAC\) là \({S_2} = \frac{1}{2}.OH.AC = \frac{1}{2}.0,5.\sqrt 3  = \frac{{\sqrt 3 }}{4}\) (\({m^2}\)).

Diện tích hình viên phân (diện tích màu tô đậm) là \[S = \frac{\pi }{3} - \frac{{\sqrt 3 }}{4} = \frac{{4\pi  - 3\sqrt 3 }}{{12}}\] (\({m^2}\)).

Thể tích bồn dầu ban đầu là \({V_1} = \pi {R^2}h = \pi {.1^2}.5 = 5\pi \,\,({m^3})\).

Thể tích phần dầu đã lấy ra là \({V_2} = 5.S = \frac{{5\left( {4\pi  - 3\sqrt 3 } \right)}}{{12}}\) (\({m^3}\)).

Thể tích dầu còn lại trong bồn chứa là \[V = {V_1} - {V_2} = 5\pi  - \frac{{5\left( {4\pi  - 3\sqrt 3 } \right)}}{{12}} \approx 12,637\].

Vậy bồn còn khoảng 12,637 m3 xăng.

Gọi chiều dài, chiều rộng của mảnh đất hình chữ nhật lần lượt là \(x \left( m \right)\), \(y \left( m \right)\).

Điều kiện: \(x > y > 0\)

Vì chu vi của mảnh đất là \(120 m\) nên \(2\left( {x + y} \right) = 120 \Leftrightarrow x + y = 60\)           \(\left( 1 \right)\)

Diện tích của mảnh dất ban đầu là \(xy \left( {{m^2}} \right)\)

Nếu tăng chiều dài thêm \(5\,m\) và tăng chiều rộng thêm \(3\,m\) thì chiều dài mảnh đất là \(x + 5 \left( m \right)\) và

chiều rộng mảnh đất là \(y + 3 \left( m \right)\). Khi đó diện tích mảnh đất tăng thêm \(245\,{m^2}\) nên

\(\left( {x + 5} \right)\left( {y + 3} \right) - xy = 245 \Rightarrow 5x + 3y = 260\)                      \(\left( 2 \right)\)

Từ \(\left( 1 \right),  \left( 2 \right)\) ta có hệ phương trình \(\left\{ \begin{array}{l}x + y = 60\\5x + 3y = 260\end{array} \right.\)

Giải hệ phương trình, ta được: \(\left\{ \begin{array}{l}x = 40\\y = 20\end{array} \right.\) ( thỏa mãn)

Vậy chiều dài và chiều rộng của mảnh đất đó là \(40\,m\) và \(20\,m\)