(1,5 điểm)
Một cuộc điều tra về thời gian một nhóm học sinh làm một bài kiểm tra trắc nghiệm cho kết quả như sau:
Thời gian (phút)
\[\left[ {0;5} \right)\]
\[\left[ {5;10} \right)\]
\[\left[ {10;15} \right)\]
\[\begin{array}{*{20}{c}}{\left[ {15,20} \right)}\end{array}\]
Tần số
1
5
9
5
Cho biết có bao nhiêu học sinh tham gia điều tra và lập bảng tần số tương đối ghép nhóm cho kết quả điều tra
Một cuộc điều tra về thời gian một nhóm học sinh làm một bài kiểm tra trắc nghiệm cho kết quả như sau:
|
Thời gian (phút) |
\[\left[ {0;5} \right)\] |
\[\left[ {5;10} \right)\] |
\[\left[ {10;15} \right)\] |
\[\begin{array}{*{20}{c}}{\left[ {15,20} \right)}\end{array}\] |
|
Tần số |
1 |
5 |
9 |
5 |
Cho biết có bao nhiêu học sinh tham gia điều tra và lập bảng tần số tương đối ghép nhóm cho kết quả điều tra
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 46 !!
Quảng cáo
Trả lời:
Có tất cả: \[1 + 5 + 9 + 5 = 20\] học sinh tham gia
Bảng tần số tương đối ghép nhóm cho kết quả trên là:
|
Thời gian (phút) |
\[\left[ {0;5} \right)\] |
\[\left[ {5;10} \right)\] |
\[\left[ {10;15} \right)\] |
\[\left[ {15,20} \right)\] |
|
Tần số tương đối |
\[5\% \] |
\[25\% \] |
\[45\% \] |
\[25\% \] |
Câu hỏi cùng đoạn
Câu 2:
Một toà nhà chung cư có 30 tầng, được đánh số lần lượt từ 1 đến 30. Bạn Bình vào thang máy ở tầng 1, bấm chọn ngẫu nhiên số một tầng để đi lên. Tính xác suất của các biến cố
A: “Bình đi lên tầng có số là một số nguyên tố”.
Một toà nhà chung cư có 30 tầng, được đánh số lần lượt từ 1 đến 30. Bạn Bình vào thang máy ở tầng 1, bấm chọn ngẫu nhiên số một tầng để đi lên. Tính xác suất của các biến cố
A: “Bình đi lên tầng có số là một số nguyên tố”.
Không gian mẫu của phép thử là \[\Omega = \left\{ {2;3;...;29;30} \right\}\]. \[\Omega \] có \(29\)phần tử.
Các kết quả của phép thử là đồng khả năng.
+ Có 10 kết quả thuận lợi cho biến cố A là:\[2;{\rm{ }}3;{\rm{ }}5;{\rm{ }}7;{\rm{ }}11;{\rm{ }}13;{\rm{ }}17;{\rm{ }}19;{\rm{ }}23;{\rm{ }}29\].
Xác suất của biến cố A là \[P\left( A \right) = \frac{{10}}{{29}}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a). Diện tích inox để làm nên chiếc xô hình trụ trên là:
S = Sxung quanh + Sđáy \( \approx 2.\pi .0,2.0,6 + {0,2^2}.\pi = 0,28.\pi \left( {{m^2}} \right)\).
Vậy diện tích inox để làm nên chiếc xô hình trụ trên \[0,28\pi \,{m^2}\]
b). Thể tích nước có trong xô là
\(V = \pi .{R^2}.\frac{2}{3}h = \pi {.0,2^2}.\frac{2}{3}0,6 = 0,016.\pi ({m^3})\)
Lời giải
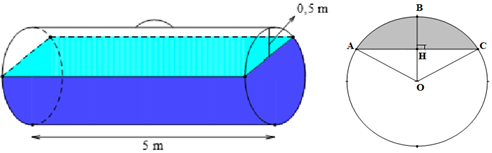
Ta có: \[OH = OB--BH\; = 1--0,5 = 0,5\] (m).
Lại có \[\cos \widehat {AOH} = \frac{{OH}}{{OA}} = \frac{{0,5}}{1} = \frac{1}{2}\]. Suy ra \[\widehat {AOH} = {60^0}\]. Suy ra \[\widehat {AOC} = {120^0}\].
Lại có \[AH = OA.\sin \widehat {AOH} = 1.\sin {60^0} = \frac{{\sqrt 3 }}{2}\]. Suy ra \[AC = 2AH = \sqrt 3 \] (m).
Diện tích hình quạt \(OAC\) là \({S_1} = \frac{{\pi .{R^2}.n}}{{360}} = \frac{{\pi {{.1}^2}.120}}{{360}} = \frac{\pi }{3}\) (\({m^2}\))
Diện tích tam giác \(OAC\) là \({S_2} = \frac{1}{2}.OH.AC = \frac{1}{2}.0,5.\sqrt 3 = \frac{{\sqrt 3 }}{4}\) (\({m^2}\)).
Diện tích hình viên phân (diện tích màu tô đậm) là \[S = \frac{\pi }{3} - \frac{{\sqrt 3 }}{4} = \frac{{4\pi - 3\sqrt 3 }}{{12}}\] (\({m^2}\)).
Thể tích bồn dầu ban đầu là \({V_1} = \pi {R^2}h = \pi {.1^2}.5 = 5\pi \,\,({m^3})\).
Thể tích phần dầu đã lấy ra là \({V_2} = 5.S = \frac{{5\left( {4\pi - 3\sqrt 3 } \right)}}{{12}}\) (\({m^3}\)).
Thể tích dầu còn lại trong bồn chứa là \[V = {V_1} - {V_2} = 5\pi - \frac{{5\left( {4\pi - 3\sqrt 3 } \right)}}{{12}} \approx 12,637\].
Vậy bồn còn khoảng 12,637 m3 xăng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.