Góc giữa hai đường thẳng \[{\Delta _1}:\,x - 2y + 15 = 0\] và \[{\Delta _2}:\,\left\{ \begin{array}{l}x = 2 - t\\y = 4 + 2t\end{array} \right.\,\,\left( {\,t \in \mathbb{R}\,} \right)\] bằng
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 2 Toán 10 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: D
Đường thẳng \[{\Delta _1}\]có một vectơ pháp tuyến là là \(\overrightarrow {{n_1}} \left( {{\mkern 1mu} 1; - 2{\mkern 1mu} } \right)\).
Đường thẳng \[{\Delta _2}\]có một vectơ chỉ phương là \(\overrightarrow u \left( { - 1;2} \right)\) suy ra \({\Delta _2}\) có một vectơ pháp tuyến là \(\overrightarrow {{n_2}} \left( {2;1} \right)\).
Ta có: \(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 1.2 + \left( { - 2} \right).1 = 0\) suy ra \({\Delta _1} \bot {\Delta _2}\).
Vậy góc giữa hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) bằng \(90^\circ \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
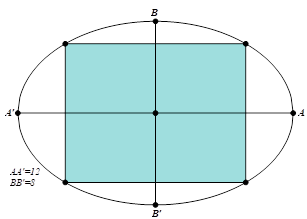
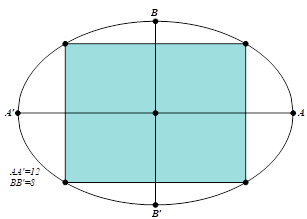
Đặt phương trình chính tắc của \(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\).
Ta có \(2a = 12 \Rightarrow a = 6\), \(2b = 8 \Rightarrow b = 4\). Suy ra \(\left( E \right):\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{16}} = 1\).
Chọn \(C\left( {{x_C};\,{y_C}} \right)\) là đỉnh hình chữ nhật và \({x_C} > 0,{y_C} > 0\).
\( \Rightarrow \frac{{x_C^2}}{{36}} + \frac{{y_C^2}}{{16}} = 1\);
Diện tích hình chữ nhật là \(S = 4{x_C}{y_C} = 48.2.\frac{{{x_C}}}{6}.\frac{{{y_C}}}{4} \le 48\left( {\frac{{x_C^2}}{{36}} + \frac{{y_C^2}}{{16}}} \right) = 48\).
Vậy diện tích trồng hoa lớn nhất có thể là \(48{m^2}\).
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
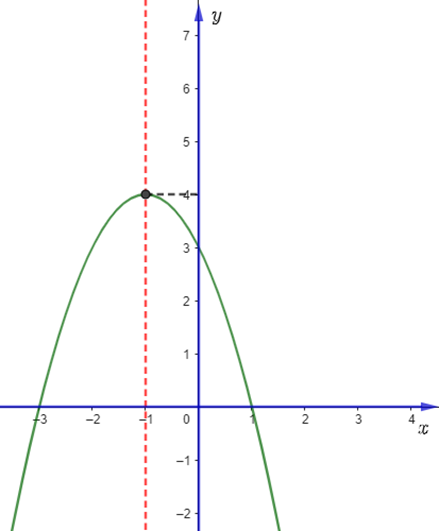
Vì Parabol có bề lõm quay xuống dưới nên \(a < 0\).
Ta gọi I là đỉnh của Parabol có \({x_I} = - \frac{b}{{2a}} = - 1 < 0\) mà \(a < 0\) nên \(b < 0\).
Đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên \(c > 0\).
Vậy \(a < 0,\,\,b < 0,\,\,c > 0\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.