Minh cần mua một mảnh vật liệu hình đa giác \({A_1}{A_2}...{A_8}\) nội tiếp elip tâm \(O\) có độ dài trục lớn và trục nhỏ lần lượt là \(10m\)và \(8m\). Đa giác có hai trục đối xứng là các trục đối xứng của elip và góc\(\widehat {{A_1}O{A_2}} = 45^\circ \). Minh cần bao nhiêu tiền để mua biết giá của vật liệu \(100\,\,000\) đồng trên \(1\,\,{m^2}\)(làm tròn đến hàng nghìn).
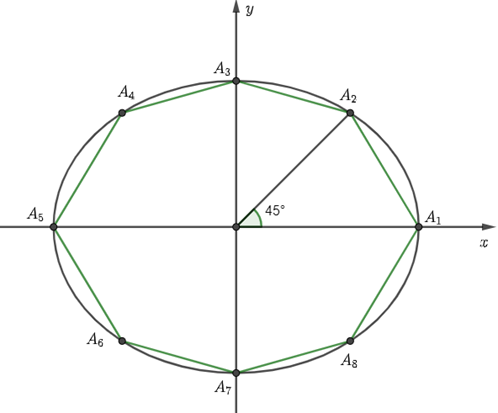
Minh cần mua một mảnh vật liệu hình đa giác \({A_1}{A_2}...{A_8}\) nội tiếp elip tâm \(O\) có độ dài trục lớn và trục nhỏ lần lượt là \(10m\)và \(8m\). Đa giác có hai trục đối xứng là các trục đối xứng của elip và góc\(\widehat {{A_1}O{A_2}} = 45^\circ \). Minh cần bao nhiêu tiền để mua biết giá của vật liệu \(100\,\,000\) đồng trên \(1\,\,{m^2}\)(làm tròn đến hàng nghìn).
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 2 Toán 10 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
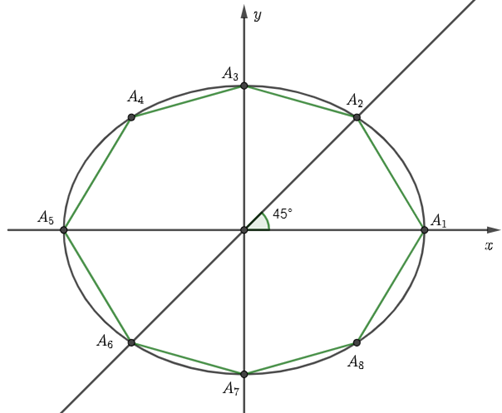
Ta có độ dài trục lớn và trục nhỏ lần lượt là \(10m\)và \(8m\) nên \(a = 5,\,b = 4\).
Suy ra phương trình của Elip \(\left( E \right):\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\).
Ta có \(\widehat {{A_1}O{A_2}} = 45^\circ \) nên \({A_2}\) là giao điểm của đường thẳng \(y = x\) và Elip \(\left( E \right)\)
Suy ra \(\frac{{{x^2}}}{{25}} + \frac{{{x^2}}}{{16}} = 1 \Rightarrow 41{x^2} = 400 \Rightarrow x = \frac{{20\sqrt {41} }}{{41}}\)
Do đó \({A_2}\left( {\frac{{20\sqrt {41} }}{{41}};\,\frac{{20\sqrt {41} }}{{41}}} \right)\).
Diện tích tam giác \({A_1}O{A_2}\) là: \({S_{{A_1}O{A_2}}} = \frac{1}{2}O{A_1}.d({A_2};O{A_1}) = \frac{1}{2}.5.\frac{{20\sqrt {41} }}{{41}} = \frac{{50\sqrt {41} }}{{41}}\,\,\left( {{m^2}} \right)\).
Diện tích tam giác \({A_2}O{A_3}\) là: \({S_{{A_2}O{A_3}}} = \frac{1}{2}O{A_3}.d({A_2};O{A_3}) = \frac{1}{2}.4.\frac{{20\sqrt {41} }}{{41}} = \frac{{40\sqrt {41} }}{{41}}\,\,\left( {{m^2}} \right)\).
\( \Rightarrow {S_{{A_1}O{A_3}{A_2}}} = {S_{{A_1}O{A_2}}} + {S_{{A_2}O{A_3}}} = \frac{{50\sqrt {41} }}{{41}}\,\, + \,\,\frac{{40\sqrt {41} }}{{41}} = \,\frac{{90\sqrt {41} }}{{41}}\,\left( {{m^2}} \right)\).
Gọi \(S\) là diện tích đa giác \({A_1}{A_2}...{A_8}\) ta có
\(S = 4{S_{{A_1}O{A_3}{A_2}}} = 4\frac{{90\sqrt {41} }}{{41}} = \frac{{360\sqrt {41} }}{{41}}\,\,\left( {{m^2}} \right)\).
Vậy số tiền Minh cần là \(\frac{{360\sqrt {41} }}{{41}}.100\,000 \approx 5\,\,622\,\,000\) (đồng).
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Kẻ \(IH \bot d\). Khi đó
\(IH = d\left( {I;d} \right) = \frac{{\left| {3.1 - 4.\left( { - 2} \right) - 1} \right|}}{{\sqrt {{3^2} + {{\left( { - 4} \right)}^2}} }} = 2\).
Diện tích tam giác \(IAB\) là: \({S_{IAB}} = \frac{1}{2}.AB.IH = \frac{1}{2}.AB.2 = AB\).
Mặt khác tam giác \(IAB\) có diện tích bằng \(4\) nên \(AB = 4\).
\( \Rightarrow AH = BH = \frac{{AB}}{2} = \frac{4}{2} = 2\).
Xét tam giác \(IAH\) vuông tại \(H\), có:
\(IA = \sqrt {I{H^2} + A{H^2}} = \sqrt {{2^2} + {2^2}} = 2\sqrt 2 \).
Do đó bán kính đường tròn \(\left( C \right)\) là \(R = 2\sqrt 2 \).
Phương trình đường tròn \(\left( C \right)\) là: \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 8\).
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Vì \(\Delta \parallel d \Rightarrow \Delta :3x - 4y + c = 4\)
Lấy điểm \(M\left( {1;1} \right) \in d\) khi đó \({d_{\left( {d;\Delta } \right)}} = {d_{\left( {M;\Delta } \right)}} = \frac{{\left| {3.1 - 4.1 + c} \right|}}{5} = 1\)
\( \Leftrightarrow \frac{{\left| {c - 1} \right|}}{5} = 1 \Leftrightarrow \left[ \begin{array}{l}c - 1 = 5\\c - 1 = - 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}c = 6\\c = - 4\end{array} \right.\) .
Phương trình đường thẳng \(\Delta :3x - 4y + 6 = 0\) hoặc \(\Delta :3x - 4y - 4 = 0\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập