(1, 0 điểm).
Một bác nông dân có một bình đựng nước chè xanh, phần chứa nước là dạng hình trụ có bán kính đáy bằng \(4\,\,{\rm{cm}}\), mực nước trong bình có chiều cao bằng \[10{\rm{ cm}}\]. Bác muốn đổ hết nước từ bình sang một cái bát uống nước, phần chứa nước là dạng nửa hình cầu có bán kính bằng \[{\rm{6 cm}}\](hình vẽ bên). Hỏi nếu đổ như vậy thì nước có bị tràn ra ngoài hay không? Vì sao?
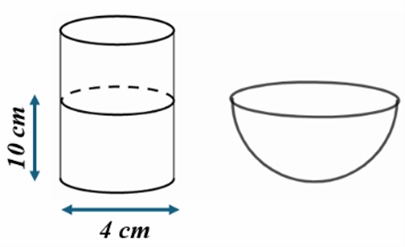
Một bác nông dân có một bình đựng nước chè xanh, phần chứa nước là dạng hình trụ có bán kính đáy bằng \(4\,\,{\rm{cm}}\), mực nước trong bình có chiều cao bằng \[10{\rm{ cm}}\]. Bác muốn đổ hết nước từ bình sang một cái bát uống nước, phần chứa nước là dạng nửa hình cầu có bán kính bằng \[{\rm{6 cm}}\](hình vẽ bên). Hỏi nếu đổ như vậy thì nước có bị tràn ra ngoài hay không? Vì sao?

Quảng cáo
Trả lời:
Thể tích nước trong bình là: \(V = \pi {R^2}h = \pi \cdot {4^2} \cdot 10\)\( = 160\pi \left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\)
Thể tích cái bát là: \({V^\prime } = \frac{1}{2}\,\, \cdot \,\,\frac{4}{3}\pi {r^3}\)\( = \frac{1}{2}\,\, \cdot \,\,\frac{4}{3}\pi \cdot {6^3}\)\( = 144\pi \left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\)
Vì \(V > V'\) nên nếu đổ như vậy thì nước có bị tràn ra ngoài.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
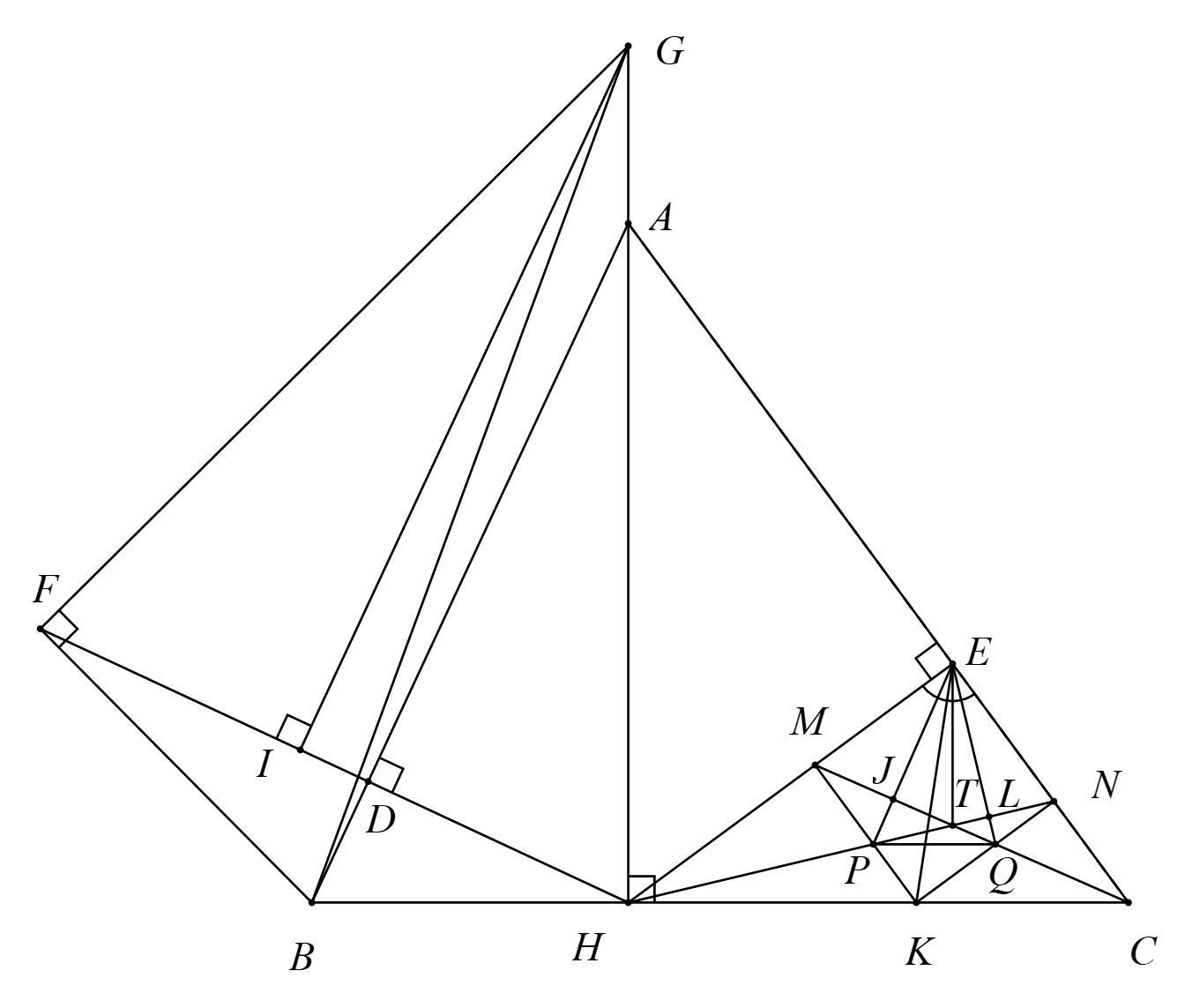
a) Ta có \(\Delta ADH\) vuông tại \(D\) nên \(\Delta ADH\) nội tiếp đường tròn đường kính \(AH\).
Ta có \(\Delta AEH\) vuông tại \(E\) nên \(\Delta AEH\) nội tiếp đường tròn đường kính \(AH\).
Bốn điểm \(A\,,\,\,D\,,\,\,H,\,\,E\) cùng thuộc đường tròn đường kính \(AH\). Hay tứ giác \(ADHE\) nội tiếp đường tròn đường kính \(AH\).
b) Vì \(GF \bot BF\) tại \(F\) nên ba điểm \(G,\,\,B,\,\,F\) thuộc đường tròn đường kính \(GB\).
\(\Delta GHB\) vuông tại \(G\) nên \(\Delta GHB\) nội tiếp đường tròn đường kính \(GB\)
Tứ giác \(GHBF\) nội tiếp đường tròn đường kính \(GB\).
Suy ra \(\widehat {GFI} = \widehat {GBH}\) (cùng chắn cung \(GH\,)\)\(\,\left( 1 \right)\)
Lại có \(GI{\rm{//}}AB\); \(AB \bot HF\) nên \(\widehat {GIF} = \widehat {CHB} = 90^\circ \,\)\(\,\left( 2 \right)\)
Từ \(\,\left( 1 \right)\) và \(\,\left( 2 \right)\) suy ra: (g.g)
Hay \(\frac{{FI}}{{HB}} = \frac{{GI}}{{GH}}\)\(\left( 3 \right)\)
Vì \(\widehat {BAH} = \widehat {BHD}\) (cùng phụ với \(\widehat {AHD}\)); \(\widehat {HDB} = \widehat {HDA} = 90^\circ \)
Do đó (g.g)
Suy ra \(\frac{{HD}}{{AD}} = \frac{{HB}}{{AH}}\) hay \(\frac{{HD}}{{HB}} = \frac{{AD}}{{AH}}\)
Mặt khác \(AD\,{\rm{//}}\,GI\) nên \(\frac{{AD}}{{GI}} = \frac{{AH}}{{HG}}\) hay \(\frac{{AD}}{{AH}} = \frac{{GI}}{{HG}}\)\(\left( 4 \right)\)
Từ \(\left( 3 \right)\) và \(\left( 4 \right)\) ta có \(\frac{{FI}}{{HB}} = \frac{{HD}}{{HB}}\) hay \(FI = HD\).
c) Gọi \(L\) là giao điểm của \(EQ\) và \(PN\). Gọi \(J\) là giao điểm của \(CM\) và \(EP\).
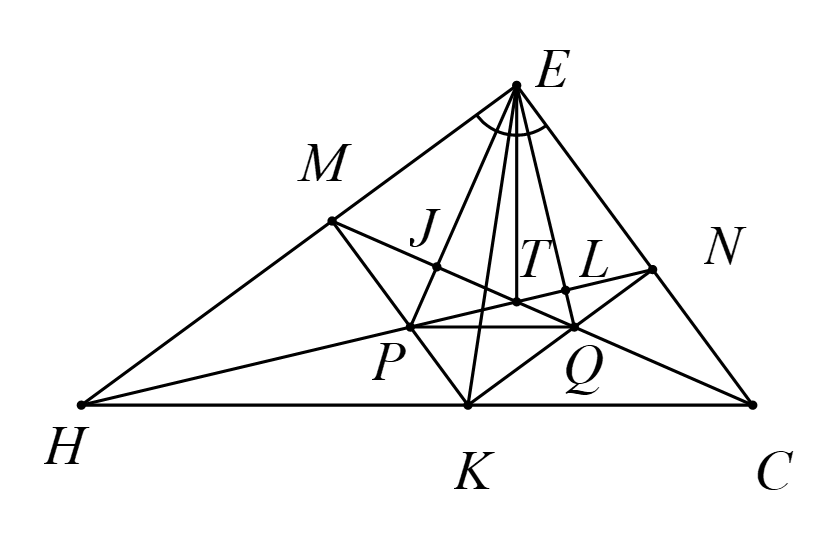
Tứ giác \(EMKN\) là hình chữ nhật ( vì \(\widehat {MEN} = \widehat {ENK} = \widehat {EMK} = 90^\circ \)).
Lại có \(EK\) là phân giác góc \(HEC\) nên \(EMKN\) là hình vuông.
Vì \(KN{\rm{//}}EH\) nên \(\frac{{CN}}{{CE}} = \frac{{NQ}}{{EM}} = \frac{{KN}}{{HE}}\) nhưng \(ME = NE\) suy ra
\(\frac{{NQ}}{{EM}} = \frac{{NQ}}{{NE}}\)\( = \frac{{KN}}{{HE}} = \frac{{EN}}{{HE}}\) hay \(\frac{{NQ}}{{NE}} = \frac{{EN}}{{HE}}\)
Lại có \(\widehat {ENQ} = \widehat {NEH} = 90^\circ \) nên (c.g.c)
Suy ra \(\widehat {NEQ} = \widehat {EHN}\) (hai góc tương ứng).
Hay \(\widehat {NEQ} + \widehat {EHN}\)\( = \widehat {EHN} + \widehat {EHN} = 90^\circ \).
Xét \(\Delta ELN\)vuông tại \(L\) suy ra \(EQ \bot HN\) tại \(L\)
Tương tự ta có \(EP \bot CM\) tại \(J\).
Xét \(\Delta EPQ\) có \(QJ\) và \(PL\) là hai đường cao cắt nhau tại \(T\) nên \(T\) là trực tâm suy ra \(ET \bot PQ\).
Lời giải
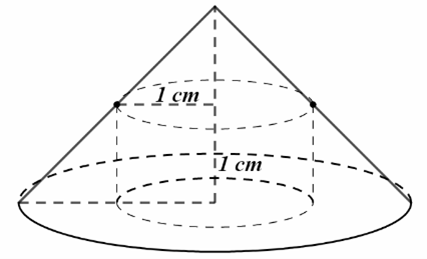
Đật \(AM = x\,\,\)\(({\rm{cm}},x > 0)\)
Khi đó chiều cao viên kẹo là \[h = OA\]\[ = x + 1\].
Áp dụng định lý Thalès, ta có: \(\frac{{AM}}{{OA}} = \frac{{EM}}{{OB}}\) hay \(\frac{x}{{x + 1}} = \frac{1}{R}\) suy ra \(R = \frac{{x + 1}}{x}\)
Thể tích viên kẹo là: \(\)
\(V = \frac{1}{3}\pi {R^2}h\)\( = \frac{1}{3}\pi {\left( {\frac{{x + 1}}{x}} \right)^2} \cdot \,\,(x + 1)\)
\( = \frac{1}{3}\pi \cdot \frac{{{x^3} + 3{x^2} + 3x + 1}}{{{x^2}}}\)\( = \pi \left( {\frac{x}{3} + 1 + \frac{1}{x} + \frac{1}{{3{x^2}}}} \right)\)
\( = \pi \left( {\frac{x}{4} + \frac{1}{x} + \frac{x}{{24}} + \frac{x}{{24}} + \frac{1}{{3{x^2}}} + 1} \right)\)
Áp dụng bất đẳng thức Cauchy, ta có:
\(\frac{x}{4} + \frac{1}{x} \ge 2\sqrt {\frac{x}{4} \cdot \frac{1}{x}} \)\( = 2 \cdot \frac{1}{2} = 1\)
\(\frac{x}{{24}} + \frac{x}{{24}} + \frac{1}{{3{x^2}}} \ge 3\sqrt[3]{{\frac{x}{{24}} \cdot \frac{x}{{24}} \cdot \frac{1}{{3{x^2}}}}}\)\( = 3 \cdot \frac{1}{{12}} = \frac{1}{4}\)
Suy ra \(V \ge \pi \left( {1 + \frac{1}{4} + 1} \right)\)\( = \frac{{9\pi }}{4}\)
Dấu xảy ra khi và chi khi \(\left\{ {\begin{array}{*{20}{l}}{\frac{x}{4} = \frac{1}{x}}\\{\frac{x}{{24}} = \frac{1}{{3{x^2}}}}\end{array}} \right.\) suy ra \(x = 2\) (TM)
Vậy chiều cao của viên kẹo là \(h = 3\,\,{\rm{cm}}\,.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.