1. Cho \(\Delta ABC\) nhọn \((AB < AC)\) nội tiếp đường tròn \((O)\). Hai đường cao BE, CF cắt nhau tại H. Gọi K là giao điểm của hai đường thẳng EF và BC.
a) Chứng minh tứ giác BFEC nội tiếp, từ đó suy ra KF.KE = KB.KC.
b) Đường thẳng AK cắt đường tròn (O) tại điểm thứ hai là M (M khác A). Gọi I là trung điểm của đoạn thẳng BC. Chứng minh ba điểm M, H, I thẳng hàng.
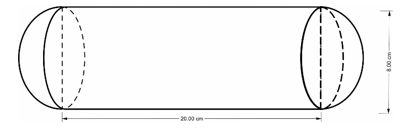
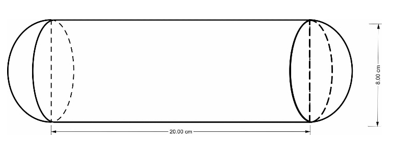
2. Một chi tiết máy gồm hai nửa hình cầu bằng nhau và một hình trụ (hình vẽ). Hãy tính thể tích của chi tiết máy đó theo các kích thước cho trên hình vẽ.
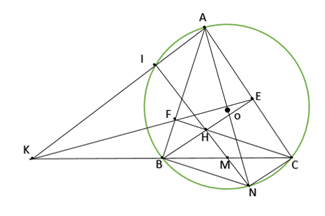
1. Cho \(\Delta ABC\) nhọn \((AB < AC)\) nội tiếp đường tròn \((O)\). Hai đường cao BE, CF cắt nhau tại H. Gọi K là giao điểm của hai đường thẳng EF và BC.
a) Chứng minh tứ giác BFEC nội tiếp, từ đó suy ra KF.KE = KB.KC.
b) Đường thẳng AK cắt đường tròn (O) tại điểm thứ hai là M (M khác A). Gọi I là trung điểm của đoạn thẳng BC. Chứng minh ba điểm M, H, I thẳng hàng.
2. Một chi tiết máy gồm hai nửa hình cầu bằng nhau và một hình trụ (hình vẽ). Hãy tính thể tích của chi tiết máy đó theo các kích thước cho trên hình vẽ.

Quảng cáo
Trả lời:
1)
a)
- Xét tứ giác \(BFEC\) có:
\(\widehat {BEC} = \widehat {CFB} = 90^\circ \)
\( \Rightarrow \) tứ giác \(BFEC\)nội tiếp ( 2 góc cùng nhìn một cạnh bằng nhau)
- Xét \(\Delta KEF\)và \(\Delta KBE\)có:
\(\widehat K\) là góc chung
\(\widehat {KCF} = \widehat {KEB}\) ( 2 góc nội tiếp cùng chắn cung BF)
\( \Rightarrow \Delta KEF\)đồng dạng với \(\Delta KBE\)
\( \Rightarrow \frac{{KF}}{{KB}} = \frac{{KC}}{{KE}} \Leftrightarrow KF.KE = KC.KB\) (đ.p.c.m) \((1)\)
b) Ta có: \(\Delta KIB\) đồng dạng \(\Delta KBA\) (g . g)
\( \Rightarrow \frac{{KI}}{{KB}} = \frac{{KC}}{{KA}} \Leftrightarrow KI.KA = KB.KC\) \((2)\)
Từ \((1)\)và \((2)\) suy ra \(KE.KF = KI.KA\)
\( \Leftrightarrow \frac{{KE}}{{KI}} = \frac{{KA}}{{KF}}\)
Mà \(\widehat K\) là góc chung
Suy ra \(\Delta KEA\) đồng dạng \(\Delta KIF\) \( \Rightarrow \widehat {KEA} = \widehat {KIF}\)
\( \Rightarrow \) tứ giác \(IAEF\)nội tiếp ( góc trong bằng góc đối ngoài )
Mặt khác \(AEHF\)nội tiếp đường tròn đường kính AH (\(\widehat {AEH} = \widehat {AFH} = {90^0}\))
Nên: \(I,A,E,F,H\)cùng thuộc một đường tròn đường kính AH
\( \Rightarrow \widehat {IHA} = 90^\circ \)
Mà : \(\widehat {NIA} = 90^\circ \) ( góc chắn nữa đường tròn )
Suy ra : \(N,I,H\) thẳng hàng
Kẻ đường kính \(AN\) của đường tròn \(\left( O \right)\) ; \(N \in \left( O \right)\)
Xét tứ giác \(BHCN\) có :
\(BH{\rm{//}}CN\) ( cùng vuông góc với AB)
\(CH{\rm{//}}BN\)( cùng vuông góc với AC)
\( \Rightarrow BHCN\)là hình bình hành
Mà M là trung điểm của BC \( \Rightarrow M \in HN\)
Suy ra \(M,I,H\) thẳng hàng2)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có: \(4xy + 2yz + 3xz = 24 \Leftrightarrow \frac{{xy}}{6} = \frac{{yz}}{{12}} = \frac{{xz}}{8} = 1\)\( \Leftrightarrow \frac{x}{2}.\frac{y}{3} + \frac{y}{3}.\frac{z}{4} + \frac{x}{2}.\frac{z}{4} = 1\)
Đặt \(\frac{x}{2} = a > 0;\frac{y}{3} = b > 0;\frac{z}{4} = c > 0 \Rightarrow ab + bc + ac = 1\)
\(\begin{array}{l}P = \frac{{4a}}{{\sqrt {4{a^2} + 4} }} + \frac{{3b}}{{\sqrt {9{b^2} + 9} }} + \frac{{4c}}{{\sqrt {16{c^2} + 16} }}\\ = \frac{{2a}}{{\sqrt {{a^2} + 1} }} + \frac{b}{{\sqrt {{b^2} + 1} }} + \frac{c}{{\sqrt {{c^2} + 1} }}\end{array}\)
\( = \frac{{2a}}{{\sqrt {{a^2} + ab + bc + ca} }} + \frac{b}{{\sqrt {{b^2} + ab + bc + ac} }} + \frac{c}{{\sqrt {{c^2} + ab + bc + ac} }}\)
\( = \frac{{2a}}{{\sqrt {\left( {a + b} \right)\left( {a + c} \right)} }} + \frac{b}{{\sqrt {\left( {a + b} \right)\left( {b + c} \right)} }} + \frac{c}{{\sqrt {\left( {a + c} \right)\left( {b + c} \right)} }}\)
\( = \sqrt {\frac{{2a}}{{a + b}}.\frac{{2a}}{{a + c}}} + \sqrt {\frac{{2b}}{{a + b}}.\frac{b}{{2\left( {b + c} \right)}}} + \sqrt {\frac{c}{{2\left( {b + c} \right)}}.\frac{{2c}}{{a + c}}} \)
Ta có :
\(\begin{array}{l}\frac{{2a}}{{a + b}} + \frac{{2a}}{{a + c}} \ge 2\sqrt {\frac{{2a}}{{a + b}}.\frac{{2a}}{{a + c}}} \\\frac{{2b}}{{a + b}} + \frac{b}{{2\left( {b + c} \right)}} \ge 2\sqrt {\frac{{2b}}{{a + b}}.\frac{b}{{2\left( {b + c} \right)}}} \\\frac{c}{{2\left( {b + c} \right)}} + \frac{{2c}}{{a + c}} \ge 2\sqrt {\frac{c}{{2\left( {b + c} \right)}}.\frac{{2c}}{{a + c}}} \end{array}\)
\(p \le \frac{1}{2}\left( {\frac{{2a}}{{a + b}} + \frac{{2a}}{{a + c}} + \frac{{2b}}{{a + b}} + \frac{b}{{2\left( {b + c} \right)}} + \frac{c}{{2\left( {b + c} \right)}} + \frac{{2c}}{{a + c}}} \right)\)
\(\begin{array}{l} \Leftrightarrow P \le \frac{1}{2}\left( {\frac{{2\left( {a + b} \right)}}{{a + b}} + \frac{{2\left( {a + c} \right)}}{{a + c}} + \frac{{b + c}}{{2(b + c)}}} \right)\\ \Leftrightarrow P \le \frac{1}{2}\left( {2 + 2 + \frac{1}{2}} \right)\\ \Leftrightarrow P \le \frac{9}{4}\end{array}\)
Dấu xảy ra khi và chỉ khi \(\left\{ \begin{array}{l}\frac{{2a}}{{a + b}} = \frac{{2a}}{{a + c}}\\\frac{{2b}}{{a + b}} = \frac{b}{{2\left( {b + c} \right)}}\\\frac{c}{{2\left( {b + c} \right)}} = \frac{{2c}}{{a + c}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = c\\a + b = 8b\\a + c = 8c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = c\\a = 7b\\a = 7c\end{array} \right.\)
\(ab + bc + ac = 1 \Leftrightarrow 7{b^2} + {b^2} + 7{b^2} = 1 \Leftrightarrow {b^2} = \frac{1}{{15}} \Leftrightarrow b = \frac{1}{{\sqrt {15} }}\)
\(\left\{ \begin{array}{l}b = \frac{1}{{\sqrt {15} }} \Rightarrow y = \frac{3}{{\sqrt {15} }}\\c = \frac{1}{{\sqrt {15} }} \Rightarrow z = \frac{4}{{\sqrt {15} }}\\a = \frac{7}{{\sqrt {15} }} \Rightarrow x = \frac{{14}}{{\sqrt {15} }}\end{array} \right.\).
Lời giải
a) \[A = \left( {\frac{{x + 2\sqrt x }}{{x + \sqrt x - 2}} + \frac{2}{{x - \sqrt x }}} \right):\frac{1}{{\sqrt x - 1}}\] ĐK: \(x \ge 0,x \ne 1\)
= \[\left( {\frac{{\sqrt x (\sqrt x + 2)}}{{(\sqrt x - 1)(\sqrt x + 2)}} + \frac{2}{{\sqrt x (\sqrt x - )}}} \right):\frac{1}{{\sqrt x - 1}}\]
= \[\left( {\frac{{x + 2}}{{(\sqrt x - 1)\sqrt x }}.\frac{{\sqrt x - 1}}{1}} \right)\]
= \[\frac{{x + 2}}{{\sqrt x }}\]
b) \(A = 3 \Leftrightarrow \frac{{x + 2}}{{\sqrt x }} = 3\)
\( \Leftrightarrow x + 2 = 3\sqrt x \)
\( \Leftrightarrow x - 3\sqrt x + 2 = 0\)
\[ \Leftrightarrow \left[ \begin{array}{l}\sqrt x = 1\\\sqrt x = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1(l)\\x = 4(n)\end{array} \right.\]
Vậy A = 3 khi x = 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.