Cho ba số thực dương x, y, z thỏa mãn \(4xy + 2yz + 3xz = 24\). Tìm giá trị lớn nhất của biểu thức \[P = \frac{{2x}}{{\sqrt {{x^2} + 4} }} + \frac{y}{{\sqrt {{y^2} + 9} }} + \frac{z}{{\sqrt {{z^2} + 16} }}\].
Cho ba số thực dương x, y, z thỏa mãn \(4xy + 2yz + 3xz = 24\). Tìm giá trị lớn nhất của biểu thức \[P = \frac{{2x}}{{\sqrt {{x^2} + 4} }} + \frac{y}{{\sqrt {{y^2} + 9} }} + \frac{z}{{\sqrt {{z^2} + 16} }}\].
Quảng cáo
Trả lời:
Ta có: \(4xy + 2yz + 3xz = 24 \Leftrightarrow \frac{{xy}}{6} = \frac{{yz}}{{12}} = \frac{{xz}}{8} = 1\)\( \Leftrightarrow \frac{x}{2}.\frac{y}{3} + \frac{y}{3}.\frac{z}{4} + \frac{x}{2}.\frac{z}{4} = 1\)
Đặt \(\frac{x}{2} = a > 0;\frac{y}{3} = b > 0;\frac{z}{4} = c > 0 \Rightarrow ab + bc + ac = 1\)
\(\begin{array}{l}P = \frac{{4a}}{{\sqrt {4{a^2} + 4} }} + \frac{{3b}}{{\sqrt {9{b^2} + 9} }} + \frac{{4c}}{{\sqrt {16{c^2} + 16} }}\\ = \frac{{2a}}{{\sqrt {{a^2} + 1} }} + \frac{b}{{\sqrt {{b^2} + 1} }} + \frac{c}{{\sqrt {{c^2} + 1} }}\end{array}\)
\( = \frac{{2a}}{{\sqrt {{a^2} + ab + bc + ca} }} + \frac{b}{{\sqrt {{b^2} + ab + bc + ac} }} + \frac{c}{{\sqrt {{c^2} + ab + bc + ac} }}\)
\( = \frac{{2a}}{{\sqrt {\left( {a + b} \right)\left( {a + c} \right)} }} + \frac{b}{{\sqrt {\left( {a + b} \right)\left( {b + c} \right)} }} + \frac{c}{{\sqrt {\left( {a + c} \right)\left( {b + c} \right)} }}\)
\( = \sqrt {\frac{{2a}}{{a + b}}.\frac{{2a}}{{a + c}}} + \sqrt {\frac{{2b}}{{a + b}}.\frac{b}{{2\left( {b + c} \right)}}} + \sqrt {\frac{c}{{2\left( {b + c} \right)}}.\frac{{2c}}{{a + c}}} \)
Ta có :
\(\begin{array}{l}\frac{{2a}}{{a + b}} + \frac{{2a}}{{a + c}} \ge 2\sqrt {\frac{{2a}}{{a + b}}.\frac{{2a}}{{a + c}}} \\\frac{{2b}}{{a + b}} + \frac{b}{{2\left( {b + c} \right)}} \ge 2\sqrt {\frac{{2b}}{{a + b}}.\frac{b}{{2\left( {b + c} \right)}}} \\\frac{c}{{2\left( {b + c} \right)}} + \frac{{2c}}{{a + c}} \ge 2\sqrt {\frac{c}{{2\left( {b + c} \right)}}.\frac{{2c}}{{a + c}}} \end{array}\)
\(p \le \frac{1}{2}\left( {\frac{{2a}}{{a + b}} + \frac{{2a}}{{a + c}} + \frac{{2b}}{{a + b}} + \frac{b}{{2\left( {b + c} \right)}} + \frac{c}{{2\left( {b + c} \right)}} + \frac{{2c}}{{a + c}}} \right)\)
\(\begin{array}{l} \Leftrightarrow P \le \frac{1}{2}\left( {\frac{{2\left( {a + b} \right)}}{{a + b}} + \frac{{2\left( {a + c} \right)}}{{a + c}} + \frac{{b + c}}{{2(b + c)}}} \right)\\ \Leftrightarrow P \le \frac{1}{2}\left( {2 + 2 + \frac{1}{2}} \right)\\ \Leftrightarrow P \le \frac{9}{4}\end{array}\)
Dấu xảy ra khi và chỉ khi \(\left\{ \begin{array}{l}\frac{{2a}}{{a + b}} = \frac{{2a}}{{a + c}}\\\frac{{2b}}{{a + b}} = \frac{b}{{2\left( {b + c} \right)}}\\\frac{c}{{2\left( {b + c} \right)}} = \frac{{2c}}{{a + c}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = c\\a + b = 8b\\a + c = 8c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = c\\a = 7b\\a = 7c\end{array} \right.\)
\(ab + bc + ac = 1 \Leftrightarrow 7{b^2} + {b^2} + 7{b^2} = 1 \Leftrightarrow {b^2} = \frac{1}{{15}} \Leftrightarrow b = \frac{1}{{\sqrt {15} }}\)
\(\left\{ \begin{array}{l}b = \frac{1}{{\sqrt {15} }} \Rightarrow y = \frac{3}{{\sqrt {15} }}\\c = \frac{1}{{\sqrt {15} }} \Rightarrow z = \frac{4}{{\sqrt {15} }}\\a = \frac{7}{{\sqrt {15} }} \Rightarrow x = \frac{{14}}{{\sqrt {15} }}\end{array} \right.\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
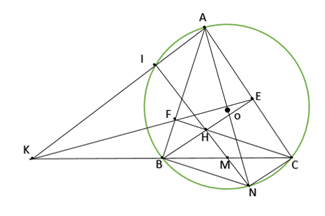
1)
a)
- Xét tứ giác \(BFEC\) có:
\(\widehat {BEC} = \widehat {CFB} = 90^\circ \)
\( \Rightarrow \) tứ giác \(BFEC\)nội tiếp ( 2 góc cùng nhìn một cạnh bằng nhau)
- Xét \(\Delta KEF\)và \(\Delta KBE\)có:
\(\widehat K\) là góc chung
\(\widehat {KCF} = \widehat {KEB}\) ( 2 góc nội tiếp cùng chắn cung BF)
\( \Rightarrow \Delta KEF\)đồng dạng với \(\Delta KBE\)
\( \Rightarrow \frac{{KF}}{{KB}} = \frac{{KC}}{{KE}} \Leftrightarrow KF.KE = KC.KB\) (đ.p.c.m) \((1)\)
b) Ta có: \(\Delta KIB\) đồng dạng \(\Delta KBA\) (g . g)
\( \Rightarrow \frac{{KI}}{{KB}} = \frac{{KC}}{{KA}} \Leftrightarrow KI.KA = KB.KC\) \((2)\)
Từ \((1)\)và \((2)\) suy ra \(KE.KF = KI.KA\)
\( \Leftrightarrow \frac{{KE}}{{KI}} = \frac{{KA}}{{KF}}\)
Mà \(\widehat K\) là góc chung
Suy ra \(\Delta KEA\) đồng dạng \(\Delta KIF\) \( \Rightarrow \widehat {KEA} = \widehat {KIF}\)
\( \Rightarrow \) tứ giác \(IAEF\)nội tiếp ( góc trong bằng góc đối ngoài )
Mặt khác \(AEHF\)nội tiếp đường tròn đường kính AH (\(\widehat {AEH} = \widehat {AFH} = {90^0}\))
Nên: \(I,A,E,F,H\)cùng thuộc một đường tròn đường kính AH
\( \Rightarrow \widehat {IHA} = 90^\circ \)
Mà : \(\widehat {NIA} = 90^\circ \) ( góc chắn nữa đường tròn )
Suy ra : \(N,I,H\) thẳng hàng
Kẻ đường kính \(AN\) của đường tròn \(\left( O \right)\) ; \(N \in \left( O \right)\)
Xét tứ giác \(BHCN\) có :
\(BH{\rm{//}}CN\) ( cùng vuông góc với AB)
\(CH{\rm{//}}BN\)( cùng vuông góc với AC)
\( \Rightarrow BHCN\)là hình bình hành
Mà M là trung điểm của BC \( \Rightarrow M \in HN\)
Suy ra \(M,I,H\) thẳng hàng2)
Lời giải
a) \[A = \left( {\frac{{x + 2\sqrt x }}{{x + \sqrt x - 2}} + \frac{2}{{x - \sqrt x }}} \right):\frac{1}{{\sqrt x - 1}}\] ĐK: \(x \ge 0,x \ne 1\)
= \[\left( {\frac{{\sqrt x (\sqrt x + 2)}}{{(\sqrt x - 1)(\sqrt x + 2)}} + \frac{2}{{\sqrt x (\sqrt x - )}}} \right):\frac{1}{{\sqrt x - 1}}\]
= \[\left( {\frac{{x + 2}}{{(\sqrt x - 1)\sqrt x }}.\frac{{\sqrt x - 1}}{1}} \right)\]
= \[\frac{{x + 2}}{{\sqrt x }}\]
b) \(A = 3 \Leftrightarrow \frac{{x + 2}}{{\sqrt x }} = 3\)
\( \Leftrightarrow x + 2 = 3\sqrt x \)
\( \Leftrightarrow x - 3\sqrt x + 2 = 0\)
\[ \Leftrightarrow \left[ \begin{array}{l}\sqrt x = 1\\\sqrt x = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1(l)\\x = 4(n)\end{array} \right.\]
Vậy A = 3 khi x = 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.