khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Ôn vào 10
  3. Toán

Câu hỏi:

12/01/2026 995 Lưu

Trong một buổi biểu diễn nghệ thuật nhằm gây quỹ từ thiện của Câu lạc bộ thiện nguyện X, ban tổ chức đã bán hết \(400\) vé. Trong đó có hai loại vé: vé loại I có mệnh giá \(100\,000\) đồng; vé loại II có mệnh giá \(75\,000\) đồng. Tổng số tiền thu được từ bán vé là \[33\,\,125\,000\] đồng. Tính số vé bán được của mỗi loại.

Xem lời giải

Câu hỏi trong đề: Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Quảng Bình năm học 2025-2026 có đáp án !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

Gọi \(x,y\) lần lượt là số vé loại I và loại II mà ban tổ chức đã bán

\(\left( {x,y \in \mathbb{N};\,x,y \le 400} \right)\)

Vì ban tổ chức đã bán được tổng cộng \(400\) vé nên ta có phương trình \(x + y = 400\,\,\left( 1 \right)\)

Vì tổng số tiền thu được từ bán vé là \(33\,\,125\,\,000\) đồng nên ta có phương trình \[100\,\,000x + 75\,\,000y = 33\,\,125\,\,000\,\] hay \(4x + 3y = 1325\,\,\,\left( 2 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có hệ phương trình \(\left\{ \begin{array}{l}x + y = 400\\4x + 3y = 1325\,\end{array} \right.\)

Giải hệ phương trình này ta được \(\left\{ \begin{array}{l}x = 125\\y = 275\end{array} \right.\) (thỏa mãn)

Vậy ban tổ chức đã bán được \(125\) vé loại I và \(275\) vé loại II.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Để đo khoảng cách từ một điểm \(B\) trên bờ sông đến một điểm \(C\) ở gốc cây trên bãi cát giữa sông, người ta chọn một điểm \(A\) cùng ở trên bờ với \(B\) sao cho từ \(A\) và \(B\) có thể nhìn thấy \(C\) (như hình bên). Bằng dụng đo, người ta đo được \(AB = 60\,m\), \(\widehat {BAC} = {45^0},\,\) \(\,\widehat {ABC} = {30^0}.\) Tính khoảng cách từ \(B\) đến \(C.\)
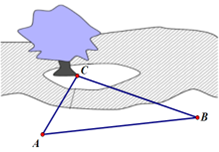
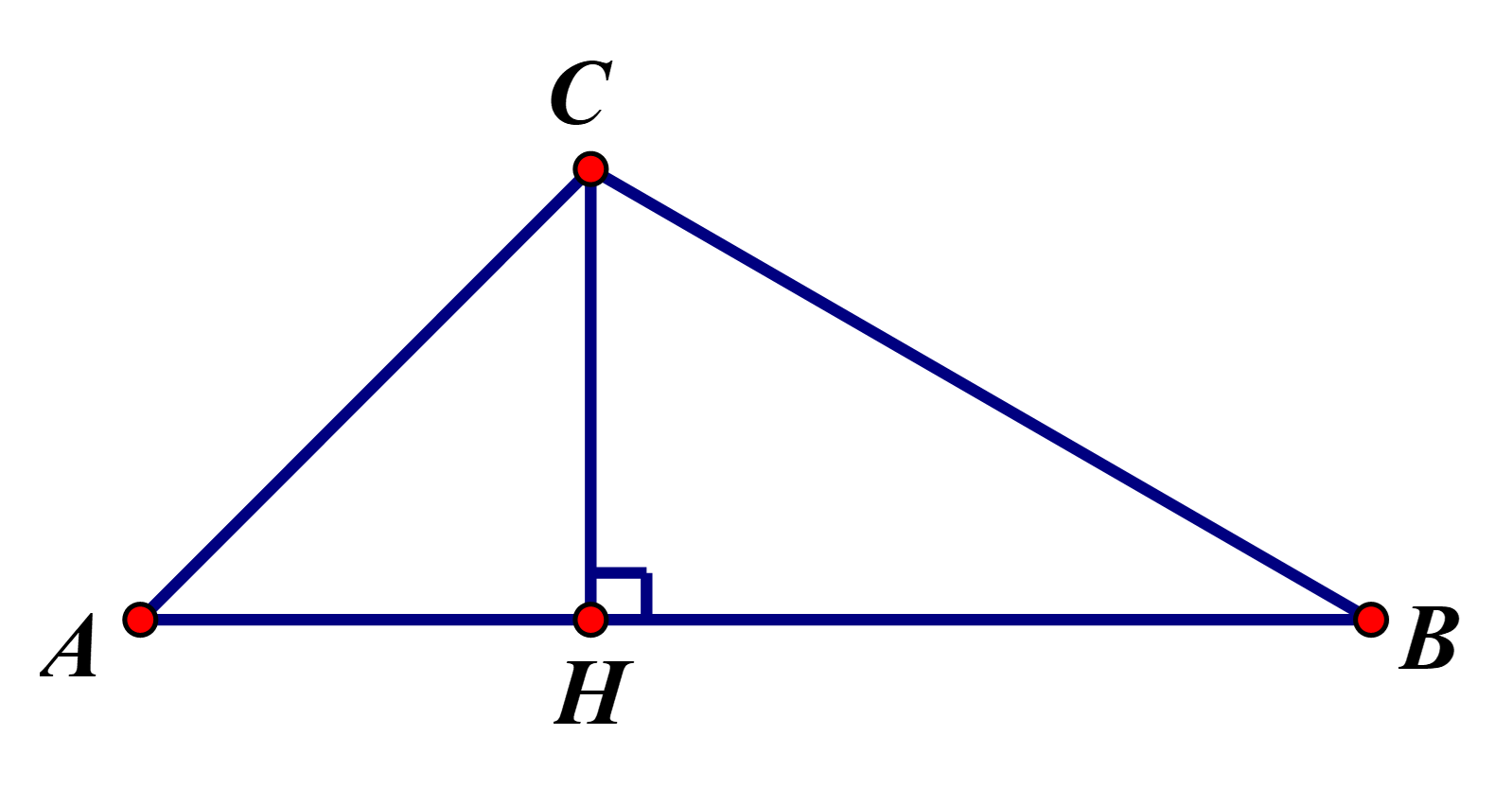
Media VietJack

Lời giải

Media VietJack

Gọi H là chân đường cao kẻ từ \(C\) đến \(AB\) của \(\Delta ABC\)

\(\Delta AHC\) vuông cân tại \(H\) nên ta có \(HA = HC.\)

\(\Delta BHC\) vuông tại \(H\) nên ta có \(HB = CH.\cot B = CH.\cot 30^\circ = \sqrt 3 .CH\)

Mà \(AH + HB = AB\) hay \(HC + \sqrt 3 .CH = 60\)

\(HC = \frac{{60}}{{1 + \sqrt 3 }}.\)

Do \(\Delta BHC\) vuông tại \(H\) nên \(BC = \frac{{HC}}{{\sin B}} = \frac{{60}}{{\left( {1 + \sqrt 3 } \right).\sin 30^\circ }} = 60\left( {\sqrt 3 - 1} \right)\,\,\left( m \right).\)

Câu 2

Người ta làm mô hình một chiếc kem gồm hai phần: phần trên có dạng một nửa hình cầu, đường kính \(AB = 50\,cm;\) phần dưới có dạng hình nón với chiều cao \(h = 120\,cm\) và đường kính đáy bằng đường kính nửa hình cầu phần trên (như hình bên). Tính thể tích của mô hình chiếc kem đó.
Media VietJack

Lời giải

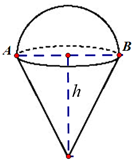
Bán kính đường tròn đáy hình nón là \(R = \frac{{AB}}{2} = 25\left( {cm} \right)\)

Thể tích khối nón là \({V_n} = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi {.25^2}.120 = 25000\pi \left( {c{m^3}} \right)\)

Vì \(R = 25\,cm\) cũng là bán kính của nửa mặt cầu.

nên thể tích của nửa khối cầu phần trên là \({V_{nc}} = \frac{1}{2}.\frac{4}{3}.\pi {R^3} = \frac{2}{3}{.25^3}\pi = \frac{{31250\pi }}{3}\left( {c{m^3}} \right)\)

Vậy thể tích của mô hình chiếc kem là

\(V = {V_n} + {V_{nc}} = 25000\pi + \frac{{31250\pi }}{3} = \frac{{106250}}{3}\pi \left( {c{m^3}} \right)\)

Câu 3

Để tham gia hội thi “Rung chuông vàng” nhân dịp kỷ niệm 94 năm thành lập Đoàn thanh niên Cộng sản Hồ Chí Minh, giáo viên chủ nhiệm lớp 9A tổ chức khảo sát kiến thức của 40 học sinh trong lớp. Điểm khảo sát của học sinh được thống kê theo bảng tần số ghép nhóm sau:

Điểm

\(\left[ {2;4} \right)\)

\(\left[ {4;6} \right)\)

\(\left[ {6;8} \right)\)

\(\left[ {8;10} \right]\)

Số lượng học sinh

6

9

18

7

a) Lập bảng tần số tương đối ghép nhóm cho bảng thống kê trên.

b) Trong các học sinh có điểm khảo sát từ \(8\) điểm trở lên có \(4\) học sinh nam. Chọn ngẫu nhiên \(2\) học sinh trong số các học sinh có điểm khảo sát đạt từ 8 trở lên. Tính xác suất của biến cố \(E\): “Hai học sinh được chọn có cùng giới tính”.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho phương trình \({x^2} - 5x - 7 = 0.\) Chứng minh phương trình đã cho có hai nghiệm phân biệt \({x_1};{x_2}\) và tính giá trị của biểu thức \(M = x_1^2 + x_2^2 - 4{x_1}{x_2}.\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Rút gọn biểu thức \(C = \frac{x}{{x - 16}} + \frac{2}{{\sqrt x + 4}} + \frac{2}{{\sqrt x - 4}}\) (với \(x \ge 0,x \ne 16\)).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Căn bậc hai của \(100\)là?

A. \(50.\)        

B. \( - 10.\)      
C. \(10.\)         
D. \( - 10\) và \(10.\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack72. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập