Để tham gia hội thi “Rung chuông vàng” nhân dịp kỷ niệm 94 năm thành lập Đoàn thanh niên Cộng sản Hồ Chí Minh, giáo viên chủ nhiệm lớp 9A tổ chức khảo sát kiến thức của 40 học sinh trong lớp. Điểm khảo sát của học sinh được thống kê theo bảng tần số ghép nhóm sau:
Điểm
\(\left[ {2;4} \right)\)
\(\left[ {4;6} \right)\)
\(\left[ {6;8} \right)\)
\(\left[ {8;10} \right]\)
Số lượng học sinh
6
9
18
7
a) Lập bảng tần số tương đối ghép nhóm cho bảng thống kê trên.
b) Trong các học sinh có điểm khảo sát từ \(8\) điểm trở lên có \(4\) học sinh nam. Chọn ngẫu nhiên \(2\) học sinh trong số các học sinh có điểm khảo sát đạt từ 8 trở lên. Tính xác suất của biến cố \(E\): “Hai học sinh được chọn có cùng giới tính”.
Để tham gia hội thi “Rung chuông vàng” nhân dịp kỷ niệm 94 năm thành lập Đoàn thanh niên Cộng sản Hồ Chí Minh, giáo viên chủ nhiệm lớp 9A tổ chức khảo sát kiến thức của 40 học sinh trong lớp. Điểm khảo sát của học sinh được thống kê theo bảng tần số ghép nhóm sau:
|
Điểm |
\(\left[ {2;4} \right)\) |
\(\left[ {4;6} \right)\) |
\(\left[ {6;8} \right)\) |
\(\left[ {8;10} \right]\) |
|
Số lượng học sinh |
6 |
9 |
18 |
7 |
a) Lập bảng tần số tương đối ghép nhóm cho bảng thống kê trên.
b) Trong các học sinh có điểm khảo sát từ \(8\) điểm trở lên có \(4\) học sinh nam. Chọn ngẫu nhiên \(2\) học sinh trong số các học sinh có điểm khảo sát đạt từ 8 trở lên. Tính xác suất của biến cố \(E\): “Hai học sinh được chọn có cùng giới tính”.
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
a. Ta có bảng tần số tương đối
|
||||||||||
|
b. Số học sinh nữ đạt từ 8 điểm trở lên là \(7 - 4 = 3\) (học sinh) Kí hiệu \(4\) học sinh nam là \({B_1};{B_2};{B_3};{B_4}\) và \(3\) học sinh nữ là \({G_1};{G_2};{G_3}\) Ta có \[\Omega = \left\{ {\left( {{B_1};{B_2}} \right);\left( {{B_1};{B_3}} \right);\left( {{B_1};{B_4}} \right);\left( {{B_1};{G_1}} \right);\left( {{B_1};{G_2}} \right);\left( {{B_1};{G_3}} \right);\left( {{B_2};{B_3}} \right);} \right.\] \[\left( {{B_2};{B_4}} \right);\left( {{B_2};{G_1}} \right);\left( {{B_2};{G_2}} \right);\left( {{B_2};{G_3}} \right);\left( {{B_3};{B_4}} \right);\left( {{B_3};{G_1}} \right);\,\,\left( {{B_3};{G_2}} \right);\]\[\left( {{B_3};{G_3}} \right);\left( {{B_4};{G_1}} \right);\left( {{B_4};{G_2}} \right);\left( {{B_4};{G_3}} \right);\left. {\left( {{G_1};{G_2}} \right);\left( {{G_1};{G_3}} \right);\left( {{G_2};{G_3}} \right)} \right\}\] Số phần tử của không gian mẫu là \(21\) hay \(n\left( \Omega \right) = 21.\) |
||||||||||
|
Các kết quả thuận lợi cho biến cố \(E\) là \[\left( {{B_1};{B_2}} \right);\left( {{B_1};{B_3}} \right);\left( {{B_1};{B_4}} \right);\left( {{B_2};{B_3}} \right);\left( {{B_2};{B_4}} \right);\left( {{B_3};{B_4}} \right);\left( {{G_1};{G_2}} \right);\left( {{G_1};{G_3}} \right);\]\[\left( {{G_2};{G_3}} \right)\] Số kết quả thuận lợi cho biến cố \(E\) là \(9\) hay \(n\left( E \right) = 9\) |
||||||||||
|
Vậy xác suất của biến cố \(E\) là \(P\left( E \right) = \frac{9}{{21}} = \frac{3}{7}.\) |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
|
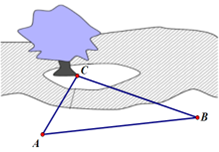
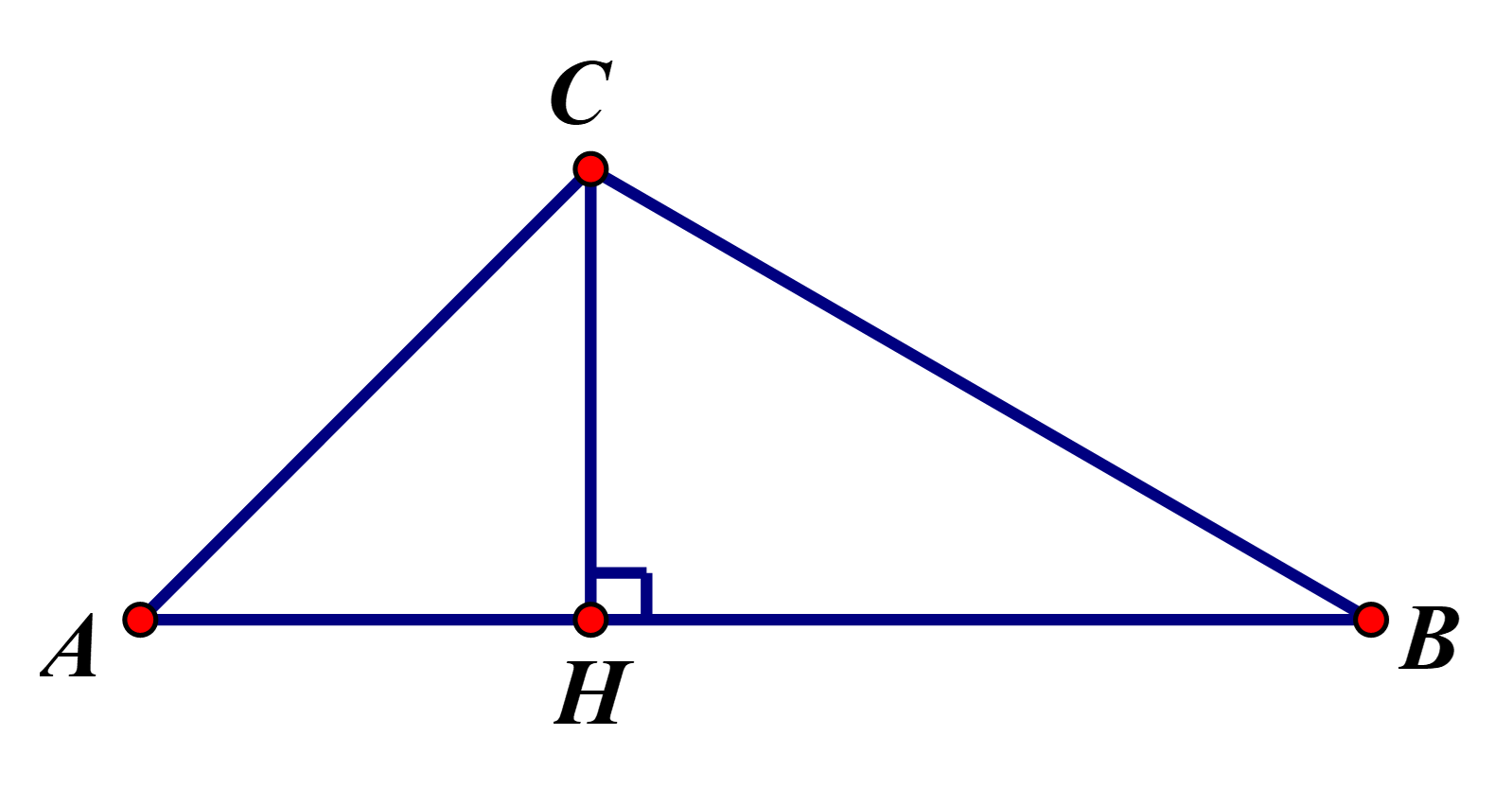
Gọi H là chân đường cao kẻ từ \(C\) đến \(AB\) của \(\Delta ABC\) \(\Delta AHC\) vuông cân tại \(H\) nên ta có \(HA = HC.\) \(\Delta BHC\) vuông tại \(H\) nên ta có \(HB = CH.\cot B = CH.\cot 30^\circ = \sqrt 3 .CH\) |
|
Mà \(AH + HB = AB\) hay \(HC + \sqrt 3 .CH = 60\) \(HC = \frac{{60}}{{1 + \sqrt 3 }}.\) |
|
Do \(\Delta BHC\) vuông tại \(H\) nên \(BC = \frac{{HC}}{{\sin B}} = \frac{{60}}{{\left( {1 + \sqrt 3 } \right).\sin 30^\circ }} = 60\left( {\sqrt 3 - 1} \right)\,\,\left( m \right).\) |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
|
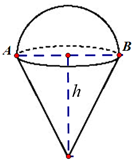
Bán kính đường tròn đáy hình nón là \(R = \frac{{AB}}{2} = 25\left( {cm} \right)\) Thể tích khối nón là \({V_n} = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi {.25^2}.120 = 25000\pi \left( {c{m^3}} \right)\) |
|
Vì \(R = 25\,cm\) cũng là bán kính của nửa mặt cầu. nên thể tích của nửa khối cầu phần trên là \({V_{nc}} = \frac{1}{2}.\frac{4}{3}.\pi {R^3} = \frac{2}{3}{.25^3}\pi = \frac{{31250\pi }}{3}\left( {c{m^3}} \right)\) |
|
Vậy thể tích của mô hình chiếc kem là \(V = {V_n} + {V_{nc}} = 25000\pi + \frac{{31250\pi }}{3} = \frac{{106250}}{3}\pi \left( {c{m^3}} \right)\) |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập