Cho parabol \[\left( P \right)\,:\,y = {x^2}\] và đường thẳng \[\left( d \right):\,y = 2x - m + 3\]. Số giá trị của \[m\] để \[\left( P \right)\] và \[\left( d \right)\] cắt nhau tại hai điểm có hoành độ \[{x_{1\,}}\,;\,{x_2}\], thoả mãn điều kiện \[{x_1}^3{x_2} + {x_1}{x_2}^3 =  - 96\] là

Chọn B

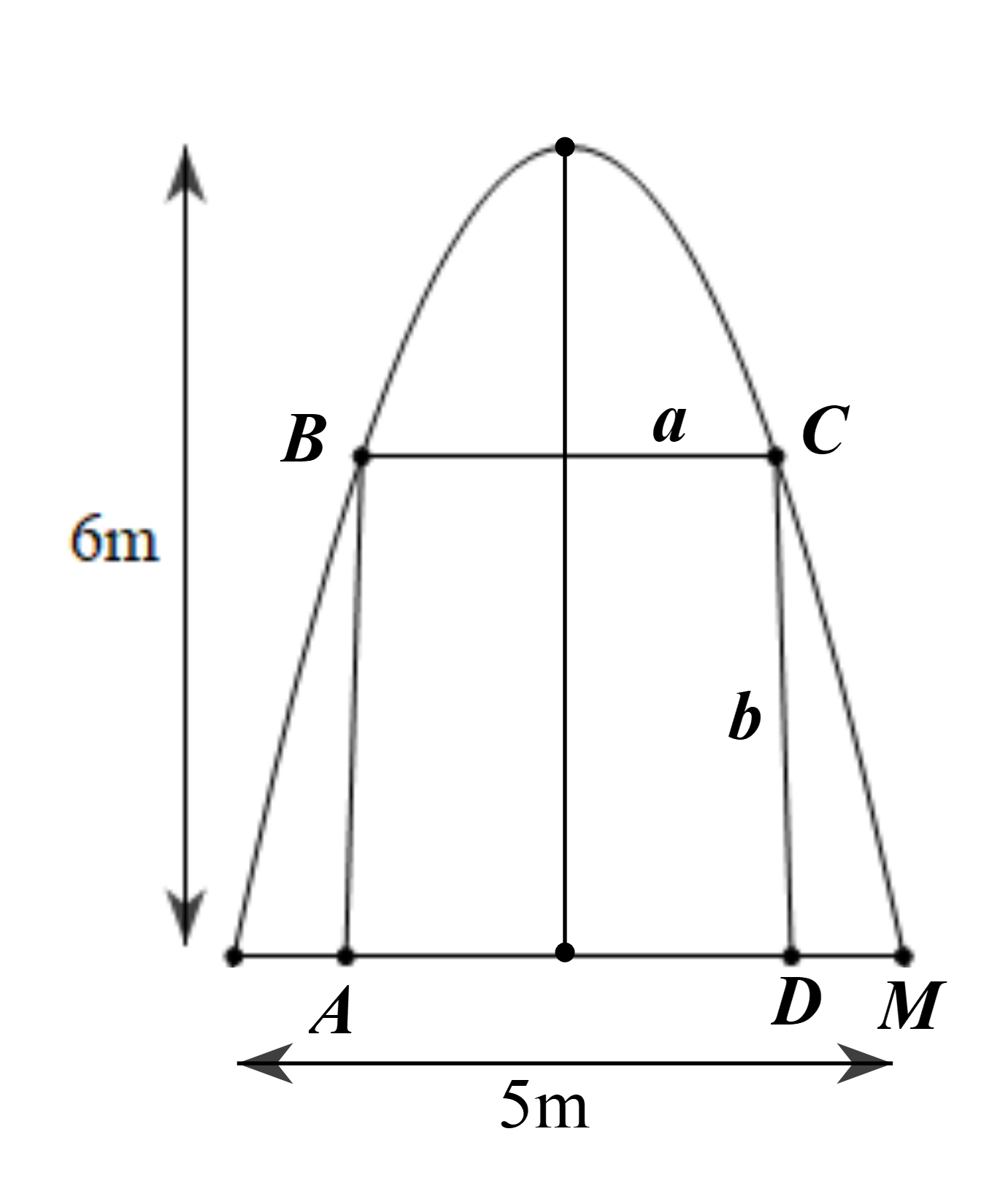
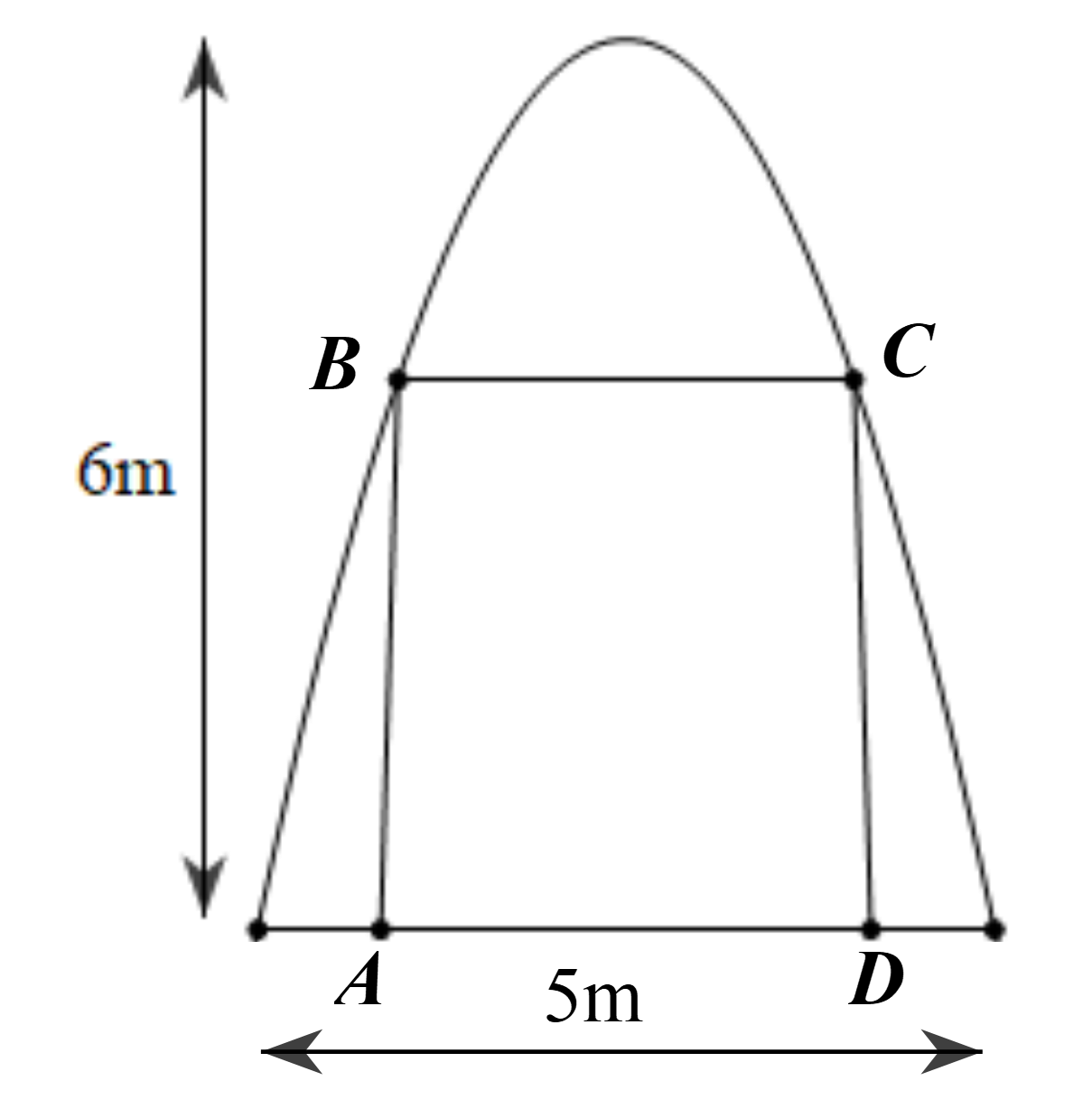
Giả sử parabol có dạng \((P):y = a{x^2}(a < 0)\)

Ta có \(M\left( {2,5; - 6} \right)\) thuộc \[\left( P \right)\] nên \( - 6 = a{.2,5^2} \Rightarrow a =  - \frac{{24}}{{25}}\)

Khi đó \[\left( P \right)\] có dạng \(y =  - \frac{{24}}{{25}}{x^2}\).

Gọi chiều rộng và chiều cao của cánh cửa lần lượt là \[a,b\]\((a > 1,\,\,b < 6)\).

Ta có \(C\left( {a; - 6 + b} \right)\) thuộc \(\left( P \right)\) nên:

\[\left\{ \begin{array}{l} - 6 + b =  - \frac{{24}}{{25}}{a^2}\\2ab = 8,64\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = \frac{{4,32}}{b}\\ - 6 + b =  - \frac{{24}}{{25}}{\left( {\frac{{4,32}}{b}} \right)^2}\end{array} \right. \Rightarrow 25{b^3} - 150{b^2} + 447,8976 = 0\]

Giải phương trình được \[{b_1} \approx  - 1,54;\,\,{b_2} \approx 5,38;\,\,{b_3} = 2,16\]

Thử lại thấy \[b = 2,16\] thỏa mãn các điều kiện.

Vậy chiều cao của khung sắt là \[2,16\,{\rm{m}}\].

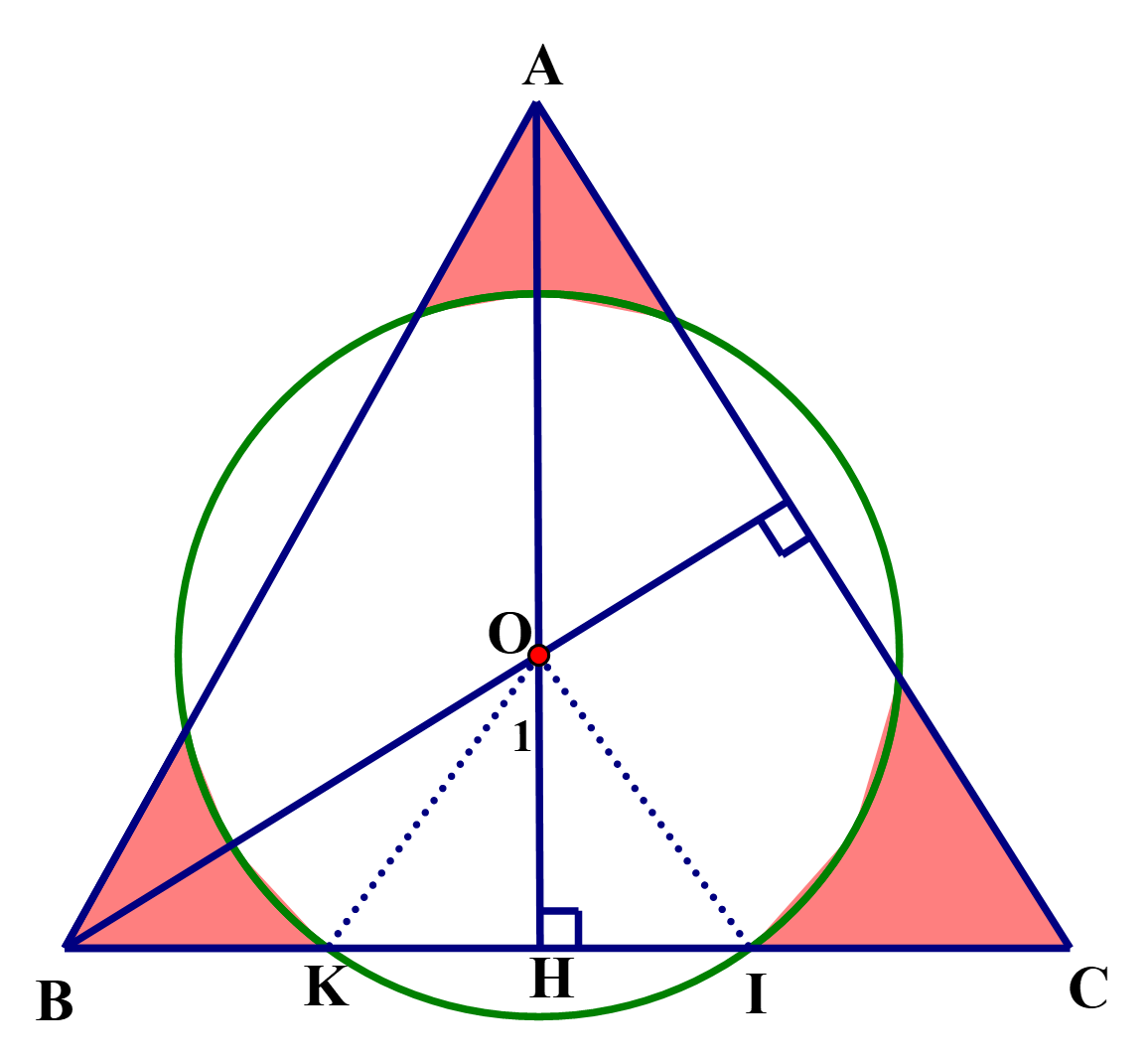
Đáp án: 16,4

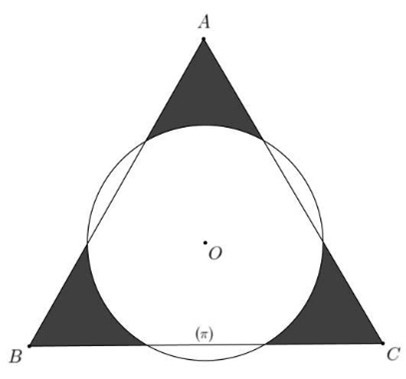
Ta có: \(AH = \frac{{12\sqrt 3 }}{2} = 6\sqrt 3 \) ( Vì \(AH\) là đường cao của \(\Delta ABC\) đều)

\(OH = \frac{1}{3}AH = \frac{1}{3}.6\sqrt 3  = 2\sqrt 3 \) ( O là trọng tâm của\(\Delta ABC\))

\[\cos {O_1} = \frac{{OH}}{{OK}} = \frac{{2\sqrt 3 }}{4} = \frac{{\sqrt 3 }}{2} \Rightarrow \widehat {{O_1}} = {30^o} \Rightarrow \widehat {KOI} = {60^o} \Rightarrow \Delta KOI\] đều

Lại có: \({S_{vp}} = {S_{qKOI}} - {S_{\Delta KOI}} = \frac{{\pi {{.4}^2}.60}}{{360}} - \frac{{{4^2}.\sqrt 4 }}{4} = \frac{8}{3}\pi  - 4\sqrt 3 \)

Diện tích cần tính là: \(S = {S_{ABC}} - {S_{tr\`o n}} + 3.{S_{VP}}\)

\( = \frac{{{{12}^2}.\sqrt 3 }}{4} - \pi {.4^2} + 3.\left( {\frac{8}{3}\pi  - 4\sqrt 3 } \right)\)

\( = 36\sqrt 3  - 16\pi  + 8\pi  - 12\sqrt 3 \) \( = 24\sqrt 3  - 8\pi  \approx 16,4\,(c{m^2})\)