Một người quan sát đứng cách một cái tháp \(12m\), nhìn thẳng đỉnh tháp và chân tháp lần lượt dưới một góc \[55^\circ \] và \[10^\circ \]so với phương nằm ngang (tham khảo hình vẽ). Chiều cao của tháp bằng bao nhiêu (làm tròn đến hàng đơn vị của m)
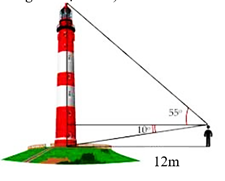
Một người quan sát đứng cách một cái tháp \(12m\), nhìn thẳng đỉnh tháp và chân tháp lần lượt dưới một góc \[55^\circ \] và \[10^\circ \]so với phương nằm ngang (tham khảo hình vẽ). Chiều cao của tháp bằng bao nhiêu (làm tròn đến hàng đơn vị của m)

Quảng cáo
Trả lời:
Đáp án:
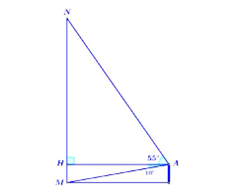
Gọi chiều cao của tháp là \(MN\), mắt người tại vị trí điểm \(A\).
Xét tam giác vuông tại \(H\) ta có: \[HM = AH.\tan \widehat {\,HAM} = 12.tan10^\circ \]
Xét tam giác vuông tại \(H\) ta có: \[HN = AH.\tan \widehat {\,HAN} = 12.tan55^\circ \]
Vậy chiều cao của tháp là: \[MN = 12.\left( {\tan 10^\circ + \tan 55^\circ } \right) \approx 19\left( m \right)\]
Đáp án: 19
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Chọn B
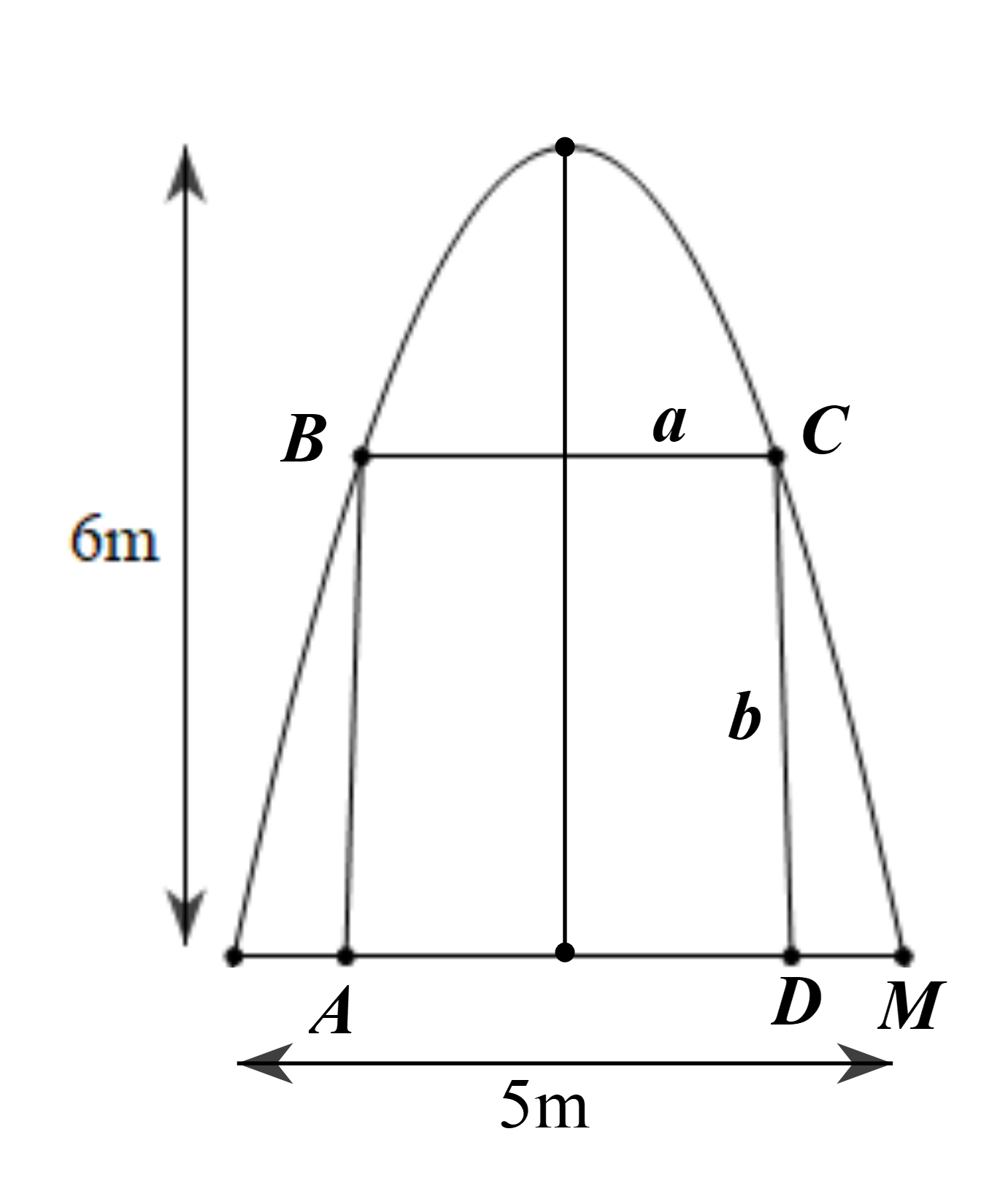
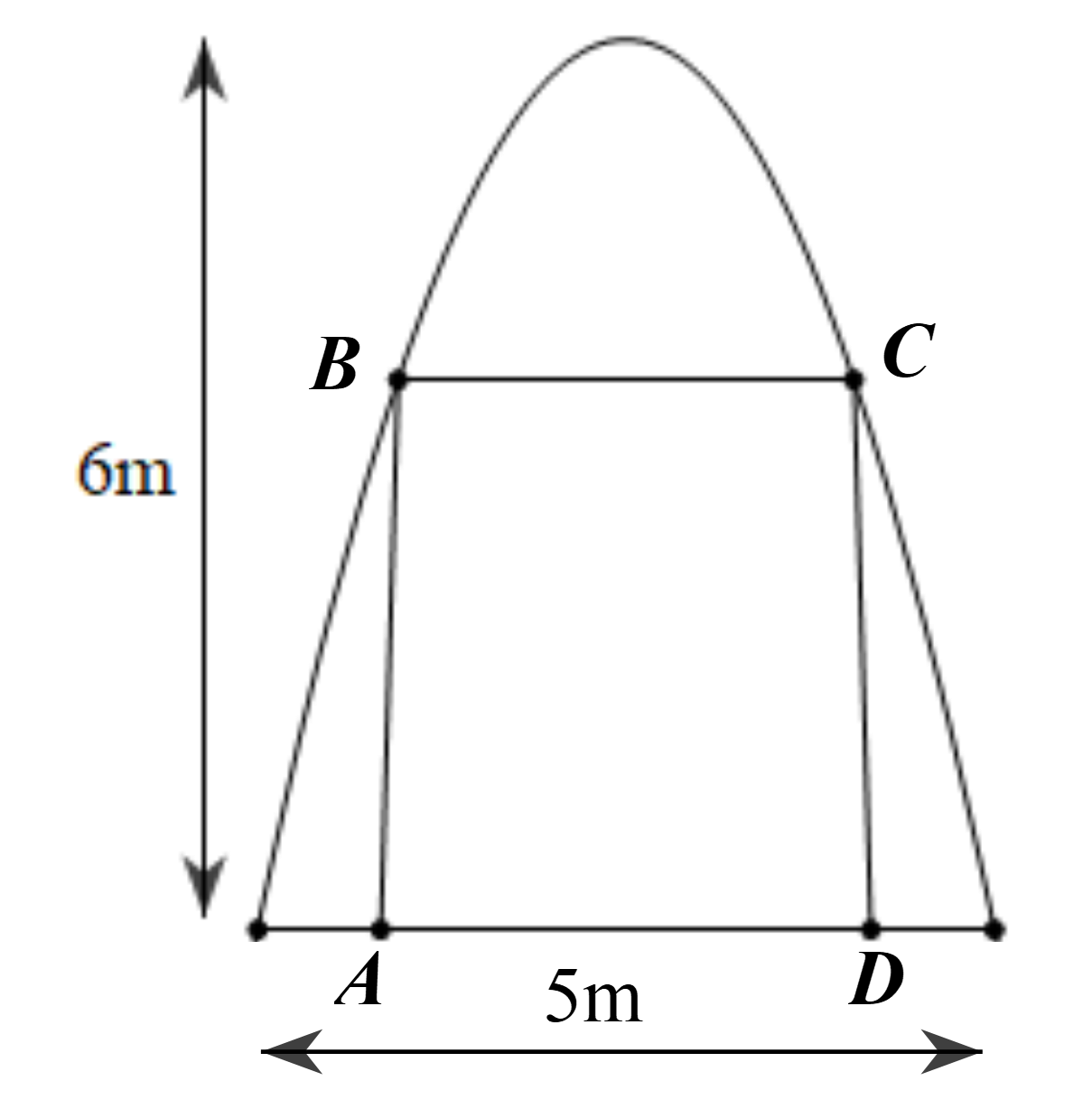
Giả sử parabol có dạng \((P):y = a{x^2}(a < 0)\)
Ta có \(M\left( {2,5; - 6} \right)\) thuộc \[\left( P \right)\] nên \( - 6 = a{.2,5^2} \Rightarrow a = - \frac{{24}}{{25}}\)
Khi đó \[\left( P \right)\] có dạng \(y = - \frac{{24}}{{25}}{x^2}\).
Gọi chiều rộng và chiều cao của cánh cửa lần lượt là \[a,b\]\((a > 1,\,\,b < 6)\).
Ta có \(C\left( {a; - 6 + b} \right)\) thuộc \(\left( P \right)\) nên:
\[\left\{ \begin{array}{l} - 6 + b = - \frac{{24}}{{25}}{a^2}\\2ab = 8,64\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = \frac{{4,32}}{b}\\ - 6 + b = - \frac{{24}}{{25}}{\left( {\frac{{4,32}}{b}} \right)^2}\end{array} \right. \Rightarrow 25{b^3} - 150{b^2} + 447,8976 = 0\]
Giải phương trình được \[{b_1} \approx - 1,54;\,\,{b_2} \approx 5,38;\,\,{b_3} = 2,16\]
Thử lại thấy \[b = 2,16\] thỏa mãn các điều kiện.
Vậy chiều cao của khung sắt là \[2,16\,{\rm{m}}\].
Lời giải
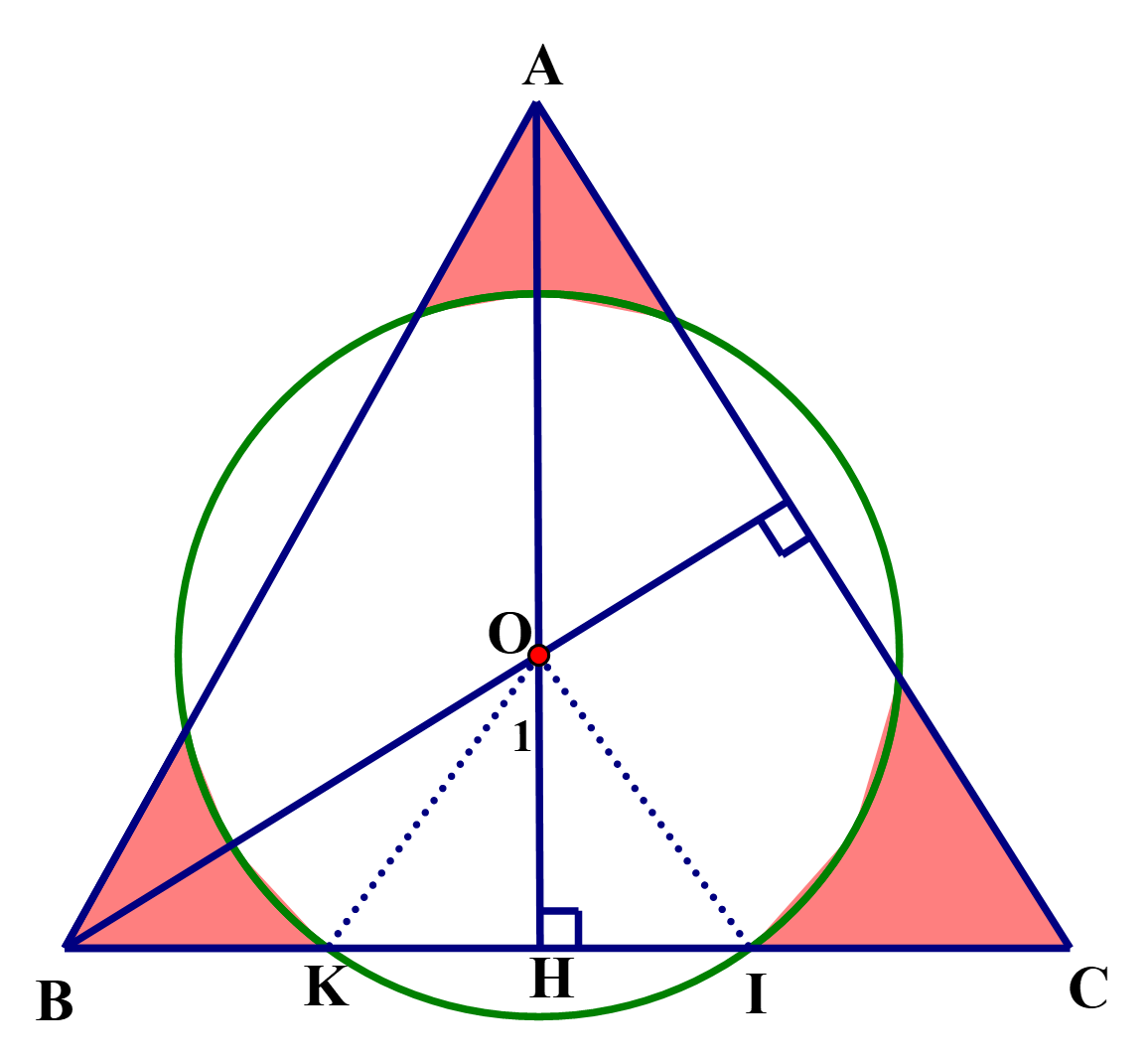
Đáp án: 16,4
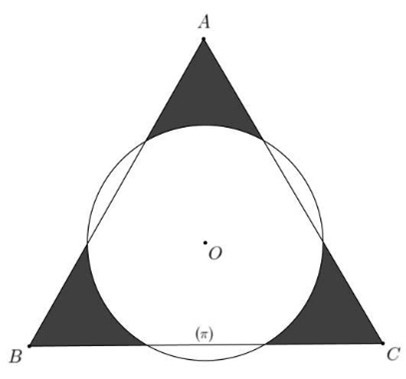
Ta có: \(AH = \frac{{12\sqrt 3 }}{2} = 6\sqrt 3 \) ( Vì \(AH\) là đường cao của \(\Delta ABC\) đều)
\(OH = \frac{1}{3}AH = \frac{1}{3}.6\sqrt 3 = 2\sqrt 3 \) ( O là trọng tâm của\(\Delta ABC\))
\[\cos {O_1} = \frac{{OH}}{{OK}} = \frac{{2\sqrt 3 }}{4} = \frac{{\sqrt 3 }}{2} \Rightarrow \widehat {{O_1}} = {30^o} \Rightarrow \widehat {KOI} = {60^o} \Rightarrow \Delta KOI\] đều
Lại có: \({S_{vp}} = {S_{qKOI}} - {S_{\Delta KOI}} = \frac{{\pi {{.4}^2}.60}}{{360}} - \frac{{{4^2}.\sqrt 4 }}{4} = \frac{8}{3}\pi - 4\sqrt 3 \)
Diện tích cần tính là: \(S = {S_{ABC}} - {S_{tr\`o n}} + 3.{S_{VP}}\)
\( = \frac{{{{12}^2}.\sqrt 3 }}{4} - \pi {.4^2} + 3.\left( {\frac{8}{3}\pi - 4\sqrt 3 } \right)\)
\( = 36\sqrt 3 - 16\pi + 8\pi - 12\sqrt 3 \) \( = 24\sqrt 3 - 8\pi \approx 16,4\,(c{m^2})\)
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.