Chứng minh phương trình \({x^2} - 12x + 35 = 0\) có hai nghiệm phân biệt \({x_1},{x_2}\). Không giải phương trình, hãy tính giá trị biểu thức \(A = x_1^2 + x_2^2 + {x_1}{x_2}\)
Chứng minh phương trình \({x^2} - 12x + 35 = 0\) có hai nghiệm phân biệt \({x_1},{x_2}\). Không giải phương trình, hãy tính giá trị biểu thức \(A = x_1^2 + x_2^2 + {x_1}{x_2}\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét phương trình \({x^2} - 12x + 35 = 0\)
\(\Delta = {( - 12)^2} - 4 \cdot 35 = 4 > 0\) nên phương trình có hai nghiệm phân biệt \({x_1},{x_2}\).
Theo Viète, ta có:
\(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 12}\\{{x_1}{x_2} = 35}\end{array}} \right.\)
Ta có:
\(A = x_1^2 + x_2^2 + {x_1}{x_2}\)
\( = x_1^2 + 2{x_1}{x_2} + x_2^2 + {x_1}{x_2} - 2{x_1}{x_2}\)
\( = {({x_1} + {x_2})^2} - {x_1}{x_2}\)
\( = {12^2} - 35\)
\( = 109\)
Vậy giá trị của biểu thức A là 109.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
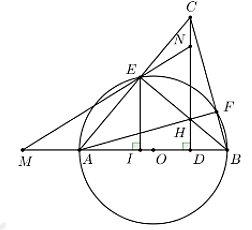
a) Ta có tam giác \(BDH\) vuông tại \(D\). Suy ra 3 điểm \(B,D,H\) cùng nằm trên đường tròn đường kính \(BH\). (1)
Ta có tam giác \(BFH\) vuông tại \(F\). Suy ra 3 điểm \(B,F,H\) cùng nằm trên đường tròn đường kính \(BH\). (2)
Từ (1) và (2) ta có tứ giác \(BDHF\) nội tiếp đường tròn đường kính \(BH\).
b) Từ \(\left\{ \begin{array}{l}\widehat {AEB} = \widehat {ADC} = 90^\circ \\\widehat A{\rm{ chung}}\end{array} \right.\) suy ra \(\Delta ABE\) và \(\Delta ACD\) đồng dạng.
Do đó \(\frac{{AE}}{{AD}} = \frac{{AB}}{{AC}}\). Tức là \(AE \cdot AC = AB \cdot AD = 2R \cdot \frac{{3R}}{2} = 3{R^2}\).
c) Ta tính được \(IO = 6\)cm, \(OD = 5\)cm.
Ta có \(EI{\rm{ // }}ND\), suy ra \(\frac{{DN}}{{EI}} = \frac{{DM}}{{MI}}\). Ta tính được \(DN = \frac{{8\left( {x + 11} \right)}}{x}\).
Vì tam giác \(DMN\) vuông tại \(D\) nên diện tích là
\(S = \frac{1}{2}DM \cdot DN = 4\frac{{{{\left( {x + 11} \right)}^2}}}{x} = 4\left( {\frac{{121}}{x} + x + 22} \right)\) (cm2)
Ta lại có \({\left( {\frac{{121}}{x} + x} \right)^2} = {\left( {\frac{{121}}{x} - x} \right)^2} + 4 \cdot \frac{{121}}{x} \cdot x \ge 484\) với mọi \(x > 0\).
Suy ra \(\frac{{121}}{x} + x \ge 22\). Dấu bằng xảy ra khi \(x = 11\).
Vậy \(x = 11\) thì diện tích của tam giác \(DMN\) nhỏ nhất.
Lời giải
|
Địa điểm |
LS |
HA |
PY |
QN |
|
Tần số |
11 |
8 |
3 |
8 |
b) Ba địa điểm được chọn nhiều nhất là: Lý Sơn, Hội An, Quy Nhơn.
Kí hiệu \(\left( {X;Y} \right)\) mô tả gia đình bạn Long chọn địa điểm X và gia đình bạn Phượng chọn địa điểm Y.
Các kết quả có thể xảy ra của phép thử là:
(LS, LS); (LS, HA); (LS, QN);
(HA, LS); (HA, HA); (HA, QN);
(QN, LS); (QN, HA); (QN, QN)
Ta có \(n\left( \Omega \right) = 9\)
Gọi biến cố A: “Hai gia đình cùng chọn một địa điểm”
Ta có \(A = \left\{ {\left( {LS;LS} \right),\left( {HA,HA} \right),\left( {QN,QN} \right)} \right\}\) . Do đó \(n\left( A \right) = 3\).
Xác suất của biến cố A là \(P\left( A \right) = \frac{3}{9} = \frac{1}{3}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập