Cho đường tròn \(\left( O \right)\) đường kính \(AB\) bằng \(2R\). Gọi \(D\) là trung điểm của \(OB\), vẽ đường thẳng \(a\) qua \(D\) và vuông góc với \(AB\). Trên đường thẳng \(a\), lấy điểm \(C\) nằm ngoài đờng tròn \(\left( O \right)\). Hai đường thẳng \(AC\), \(BC\) cắt đường tròn \(\left( O \right)\) lần lượt tại \(E,F\) (với \(E\)khác \(A\), \(F\) khác \(B\)). Gọi \(H\) là giao điểm của \(AF\) và \(CD\).
a) Chứng minh tứ giác \(BDHF\) nội tiếp.
b) Chứng minh \(AE \cdot AC = 3{R^2}\).
c) Vẽ \(EI\) vuông góc với \(AB\) tại \(I\), cho biết \(EI = 8{\rm{cm}}\) và \(R = 10{\rm{cm}}\). Đường thẳng qua \(E\) cắt tia \(DA,DC\) lần lượt tại \(M,N\). Đặt \(IM = x\) (cm), tính \(DN\) theo \(x\) và tìm \(x\) để diện tích của tam giác \(DMN\) nhỏ nhất.
Cho đường tròn \(\left( O \right)\) đường kính \(AB\) bằng \(2R\). Gọi \(D\) là trung điểm của \(OB\), vẽ đường thẳng \(a\) qua \(D\) và vuông góc với \(AB\). Trên đường thẳng \(a\), lấy điểm \(C\) nằm ngoài đờng tròn \(\left( O \right)\). Hai đường thẳng \(AC\), \(BC\) cắt đường tròn \(\left( O \right)\) lần lượt tại \(E,F\) (với \(E\)khác \(A\), \(F\) khác \(B\)). Gọi \(H\) là giao điểm của \(AF\) và \(CD\).
a) Chứng minh tứ giác \(BDHF\) nội tiếp.
b) Chứng minh \(AE \cdot AC = 3{R^2}\).
c) Vẽ \(EI\) vuông góc với \(AB\) tại \(I\), cho biết \(EI = 8{\rm{cm}}\) và \(R = 10{\rm{cm}}\). Đường thẳng qua \(E\) cắt tia \(DA,DC\) lần lượt tại \(M,N\). Đặt \(IM = x\) (cm), tính \(DN\) theo \(x\) và tìm \(x\) để diện tích của tam giác \(DMN\) nhỏ nhất.
Quảng cáo
Trả lời:
Giải bởi Vietjack
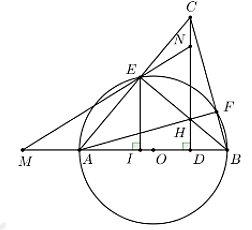
a) Ta có tam giác \(BDH\) vuông tại \(D\). Suy ra 3 điểm \(B,D,H\) cùng nằm trên đường tròn đường kính \(BH\). (1)
Ta có tam giác \(BFH\) vuông tại \(F\). Suy ra 3 điểm \(B,F,H\) cùng nằm trên đường tròn đường kính \(BH\). (2)
Từ (1) và (2) ta có tứ giác \(BDHF\) nội tiếp đường tròn đường kính \(BH\).
b) Từ \(\left\{ \begin{array}{l}\widehat {AEB} = \widehat {ADC} = 90^\circ \\\widehat A{\rm{ chung}}\end{array} \right.\) suy ra \(\Delta ABE\) và \(\Delta ACD\) đồng dạng.
Do đó \(\frac{{AE}}{{AD}} = \frac{{AB}}{{AC}}\). Tức là \(AE \cdot AC = AB \cdot AD = 2R \cdot \frac{{3R}}{2} = 3{R^2}\).
c) Ta tính được \(IO = 6\)cm, \(OD = 5\)cm.
Ta có \(EI{\rm{ // }}ND\), suy ra \(\frac{{DN}}{{EI}} = \frac{{DM}}{{MI}}\). Ta tính được \(DN = \frac{{8\left( {x + 11} \right)}}{x}\).
Vì tam giác \(DMN\) vuông tại \(D\) nên diện tích là
\(S = \frac{1}{2}DM \cdot DN = 4\frac{{{{\left( {x + 11} \right)}^2}}}{x} = 4\left( {\frac{{121}}{x} + x + 22} \right)\) (cm2)
Ta lại có \({\left( {\frac{{121}}{x} + x} \right)^2} = {\left( {\frac{{121}}{x} - x} \right)^2} + 4 \cdot \frac{{121}}{x} \cdot x \ge 484\) với mọi \(x > 0\).
Suy ra \(\frac{{121}}{x} + x \ge 22\). Dấu bằng xảy ra khi \(x = 11\).
Vậy \(x = 11\) thì diện tích của tam giác \(DMN\) nhỏ nhất.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
Địa điểm |
LS |
HA |
PY |
QN |
|
Tần số |
11 |
8 |
3 |
8 |
b) Ba địa điểm được chọn nhiều nhất là: Lý Sơn, Hội An, Quy Nhơn.
Kí hiệu \(\left( {X;Y} \right)\) mô tả gia đình bạn Long chọn địa điểm X và gia đình bạn Phượng chọn địa điểm Y.
Các kết quả có thể xảy ra của phép thử là:
(LS, LS); (LS, HA); (LS, QN);
(HA, LS); (HA, HA); (HA, QN);
(QN, LS); (QN, HA); (QN, QN)
Ta có \(n\left( \Omega \right) = 9\)
Gọi biến cố A: “Hai gia đình cùng chọn một địa điểm”
Ta có \(A = \left\{ {\left( {LS;LS} \right),\left( {HA,HA} \right),\left( {QN,QN} \right)} \right\}\) . Do đó \(n\left( A \right) = 3\).
Xác suất của biến cố A là \(P\left( A \right) = \frac{3}{9} = \frac{1}{3}\)
Lời giải
Bán kính hình cầu là \(R = \frac{{48}}{2} = 24\)(cm)
Thể tích muối trong thúng là \(V = \frac{1}{3}\pi \cdot {24^2} \cdot 14 + \frac{1}{2} \cdot \frac{4}{3}\pi \cdot {24^3} = 11904\pi \)(cm3)
Ta có \(\frac{V}{{{V_1}}} = \frac{{11904\pi }}{{3000\pi }} = 3,968\).
Vậy bác Hoa cần phải sử dụng ít nhất 4 thùng nhựa.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập
Vũ Cường Nguyễn
nếu vẽ hình E nằm bên phía OB đc ko ạ thì nó ra kết quá khác