Một công ty du lịch cần chọn 3 trong 4 địa điểm là Lý Sơn (LS), Hội An (HA), Phú Yên (PY), Quy Nhơn (QN) để tổ chức các chuyến du lịch nhân dịp lễ Quốc Khánh 2-9. Công ty tiến hành khảo sát 30 gia đình. Kết quả khảo sát được liệt kê dưới đây:
LS
HA
PY
LS
LS
PY
HA
QN
HA
LS
QN
LS
HA
PY
LS
LS
QN
HA
HA
LS
HA
QN
QN
QN
LS
LS
HA
QN
LS
QN
a) Hãy lập bảng tần số cho kết quả khảo sát trên
b) Ba địa điểm được chọn nhiều nhất theo kết quả khảo sát trên được công ty chọn để tổ chức chuyến du lịch. Gia đình bạn Long và gia đình bạn Phượng mỗi gia đình chọn ngẫu nhiên một trong ba địa điểm đó để du lịch. Tính xác suất để cả 2 gia đình chọn cùng một địa điểm.
Một công ty du lịch cần chọn 3 trong 4 địa điểm là Lý Sơn (LS), Hội An (HA), Phú Yên (PY), Quy Nhơn (QN) để tổ chức các chuyến du lịch nhân dịp lễ Quốc Khánh 2-9. Công ty tiến hành khảo sát 30 gia đình. Kết quả khảo sát được liệt kê dưới đây:
|
LS |
HA |
PY |
LS |
LS |
PY |
HA |
QN |
HA |
LS |
|
QN |
LS |
HA |
PY |
LS |
LS |
QN |
HA |
HA |
LS |
|
HA |
QN |
QN |
QN |
LS |
LS |
HA |
QN |
LS |
QN |
a) Hãy lập bảng tần số cho kết quả khảo sát trên
b) Ba địa điểm được chọn nhiều nhất theo kết quả khảo sát trên được công ty chọn để tổ chức chuyến du lịch. Gia đình bạn Long và gia đình bạn Phượng mỗi gia đình chọn ngẫu nhiên một trong ba địa điểm đó để du lịch. Tính xác suất để cả 2 gia đình chọn cùng một địa điểm.
Quảng cáo
Trả lời:
|
Địa điểm |
LS |
HA |
PY |
QN |
|
Tần số |
11 |
8 |
3 |
8 |
b) Ba địa điểm được chọn nhiều nhất là: Lý Sơn, Hội An, Quy Nhơn.
Kí hiệu \(\left( {X;Y} \right)\) mô tả gia đình bạn Long chọn địa điểm X và gia đình bạn Phượng chọn địa điểm Y.
Các kết quả có thể xảy ra của phép thử là:
(LS, LS); (LS, HA); (LS, QN);
(HA, LS); (HA, HA); (HA, QN);
(QN, LS); (QN, HA); (QN, QN)
Ta có \(n\left( \Omega \right) = 9\)
Gọi biến cố A: “Hai gia đình cùng chọn một địa điểm”
Ta có \(A = \left\{ {\left( {LS;LS} \right),\left( {HA,HA} \right),\left( {QN,QN} \right)} \right\}\) . Do đó \(n\left( A \right) = 3\).
Xác suất của biến cố A là \(P\left( A \right) = \frac{3}{9} = \frac{1}{3}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
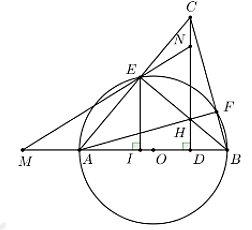
a) Ta có tam giác \(BDH\) vuông tại \(D\). Suy ra 3 điểm \(B,D,H\) cùng nằm trên đường tròn đường kính \(BH\). (1)
Ta có tam giác \(BFH\) vuông tại \(F\). Suy ra 3 điểm \(B,F,H\) cùng nằm trên đường tròn đường kính \(BH\). (2)
Từ (1) và (2) ta có tứ giác \(BDHF\) nội tiếp đường tròn đường kính \(BH\).
b) Từ \(\left\{ \begin{array}{l}\widehat {AEB} = \widehat {ADC} = 90^\circ \\\widehat A{\rm{ chung}}\end{array} \right.\) suy ra \(\Delta ABE\) và \(\Delta ACD\) đồng dạng.
Do đó \(\frac{{AE}}{{AD}} = \frac{{AB}}{{AC}}\). Tức là \(AE \cdot AC = AB \cdot AD = 2R \cdot \frac{{3R}}{2} = 3{R^2}\).
c) Ta tính được \(IO = 6\)cm, \(OD = 5\)cm.
Ta có \(EI{\rm{ // }}ND\), suy ra \(\frac{{DN}}{{EI}} = \frac{{DM}}{{MI}}\). Ta tính được \(DN = \frac{{8\left( {x + 11} \right)}}{x}\).
Vì tam giác \(DMN\) vuông tại \(D\) nên diện tích là
\(S = \frac{1}{2}DM \cdot DN = 4\frac{{{{\left( {x + 11} \right)}^2}}}{x} = 4\left( {\frac{{121}}{x} + x + 22} \right)\) (cm2)
Ta lại có \({\left( {\frac{{121}}{x} + x} \right)^2} = {\left( {\frac{{121}}{x} - x} \right)^2} + 4 \cdot \frac{{121}}{x} \cdot x \ge 484\) với mọi \(x > 0\).
Suy ra \(\frac{{121}}{x} + x \ge 22\). Dấu bằng xảy ra khi \(x = 11\).
Vậy \(x = 11\) thì diện tích của tam giác \(DMN\) nhỏ nhất.
Lời giải
Gọi vận tốc của ô tô là \(x\) (km/h), \(x > 0\).
Khi đó vận tốc của xe máy là \(x - 10\) (km/h).
Thời gian ô tô đi hết quãng đường là \(\frac{{160}}{x}\) (giờ).
Thời gian xe máy đi hết quãng đường là \(\frac{{160}}{{x - 10}}\) (giờ).
Xe ô tô đến trước xe máy 48 phút = \(\frac{4}{5}\) giờ.
Ta có phương trình:
\(\frac{{160}}{{x - 10}} - \frac{{160}}{x} = \frac{4}{5}\)
Giải phương trình:
\(160 \cdot 5x - 160 \cdot 5(x - 10) = 4x(x - 10)\)
\(4{x^2} - 40x - 8000 = 0\)
Giải phương trình \(4{x^2} - 40x - 8000 = 0\) ta được \(x = 50\) (tmđk) và \(x = - 40\) (loại).
Vậy vận tốc của ô tô là 50 km/h và vận tốc của xe máy là 40 km/h.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.