Cho điểm M thuộc nửa đường tròn (O) đường kính \(AB = 2R\)(M khác A và B). Kẻ các tiếp tuyến Ax, By với nửa đường tròn (Ax và By cùng thuộc nửa mặt phẳng bờ AB chứa nửa đường tròn). Tiếp tuyến tại M của (O) cắt Ax, By lần lượt tại E và F, AF cắt BE tại K.
1. Chứng minh: \(AE.BF = {R^2}.\)
2. Kéo dài MK cắt AB tại H. Chứng minh K là trung điểm của MH.
Cho điểm M thuộc nửa đường tròn (O) đường kính \(AB = 2R\)(M khác A và B). Kẻ các tiếp tuyến Ax, By với nửa đường tròn (Ax và By cùng thuộc nửa mặt phẳng bờ AB chứa nửa đường tròn). Tiếp tuyến tại M của (O) cắt Ax, By lần lượt tại E và F, AF cắt BE tại K.
1. Chứng minh: \(AE.BF = {R^2}.\)
2. Kéo dài MK cắt AB tại H. Chứng minh K là trung điểm của MH.
Quảng cáo
Trả lời:
Giải bởi Vietjack
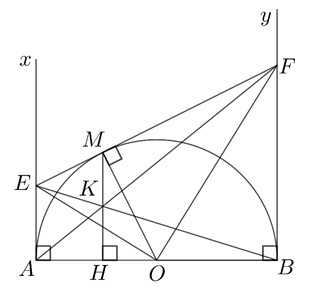
Ta có \(OE \bot {\rm{OF}}\)
\(O{M^2} = ME.MF\)
\(ME.MF = {R^2}\)
\( \Rightarrow AE.BF = {R^2}\)\(Ax//By \Rightarrow \frac{{AE}}{{BF}} = \frac{{EK}}{{KB}}\,\,\,\,\)(hệ quả định lí Talet)
Do \(AE = EM;\,\,BF = MF\) (T/c tiếp tuyến)
\( \Rightarrow \frac{{EM}}{{MF}} = \frac{{EK}}{{KB}}\,\, \Rightarrow MH//{\rm{Ax//By}}\)(Talet đảo)
Do đó \(\frac{{KH}}{{AE}} = \frac{{KB}}{{BE}}\,\, = \frac{{KF}}{{FA}} = \frac{{MK}}{{AE}}\) (Talet)
Suy ra \(KH = MK\)Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi số học sinh dự thi của hai trường A, B lần lượt là \(x,\,y\) (học sinh) \(\left( {x,y \in {\mathbb{N}^*}} \right)\)
Số học sinh trúng tuyển chiếm 40% nên ta có
\(\left( {x + y} \right)40\% = 22 \Leftrightarrow x + y = 55\)
Trường A có số học sinh trúng tuyển là \(50\% x = \frac{1}{2}x\)
Trường B có số học sinh trúng tuyển là \(28\% y = \frac{7}{{25}}y\)
Cả hai trường có 22 học sinh trúng tuyển
\(\frac{1}{2}x + \frac{7}{{25}}y = 22 \Leftrightarrow 25x + 14y = 1100\)
Hệ phương trình \(\left\{ \begin{array}{l}x + y = 55\\25x + 14y = 1100\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 30\\y = 25\end{array} \right.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
\(1.\,\,\,\left\{ \begin{array}{l}\left| {x + 2} \right| + 4\sqrt {y - 1} = 5\\3\left| {x + 2} \right| - 2\sqrt {y - 1} = 1\end{array} \right.\,\,\,\,\,\,\,\,\,\left( {y \ge 1} \right)\)
\[ \Leftrightarrow \left\{ \begin{array}{l}\left| {x + 2} \right| + 4\sqrt {y - 1} = 5\\6\left| {x + 2} \right| - 4\sqrt {y - 1} = 2\end{array} \right.\]
\[ \Leftrightarrow \left\{ \begin{array}{l}\left| {x + 2} \right| + 4\sqrt {y - 1} = 5\\7\left| {x + 2} \right| = 7\end{array} \right.\]
\[ \Leftrightarrow \left\{ \begin{array}{l}\sqrt {y - 1} = 1\\\left| {x + 2} \right| = 1\end{array} \right.\]
\[ \Leftrightarrow \left\{ \begin{array}{l}y - 1 = 1\\x + 2 = \pm 1\end{array} \right.\]
Nghiệm: (– 1; 2), (– 3; 2).\(\begin{array}{l}2.\,\,{x^2} + \left( {3 - \sqrt {{x^2} + 2} } \right)x = 1 + 2\sqrt {{x^2} + 2} \\ \Leftrightarrow {x^2} + 3x - 1 = \left( {x + 2} \right)\sqrt {{x^2} + 2} \\ \Leftrightarrow {x^2} + 2 - \left( {x + 2} \right)\sqrt {{x^2} + 2} + 3\left( {x - 1} \right) = 0\end{array}\)
Đặt \(t = \sqrt {{x^2} + 2} \Rightarrow t \ge \sqrt 2 \)
Phương trình trở thành
\({t^2} - \left( {x + 2} \right)t + 3\left( {x - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}t = 3\\t = x - 1\end{array} \right.\)
Suy ra \(\left[ \begin{array}{l}\sqrt {{x^2} + 2} = 3\\\sqrt {{x^2} + 2} = x - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^2} = 7 \Leftrightarrow x = \pm \sqrt 7 \\\left\{ \begin{array}{l}x - 1 \ge 0\\2x = - 1\end{array} \right. \Leftrightarrow x = \frac{{ - 1}}{2}\,\,\left( {loai} \right)\end{array} \right.\)
Phương trình có nghiệm \(x = \pm \sqrt 7 \).Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập