Cho bảng tần số tương đối ghép nhóm như sau:

Nhóm	\[\left[ {4;8} \right)\]	\[\left[ {8;12} \right)\]	\[\left[ {12;16} \right)\]	\[\left[ {16;20} \right)\]
Tần số tương đối	\[30\% \]	\[14\% \]	\[21\% \]	\[35\% \]

                        Để vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng, ta dùng giá trị nào đại diện cho nhóm số liệu \[\left[ {8;12} \right)\]?

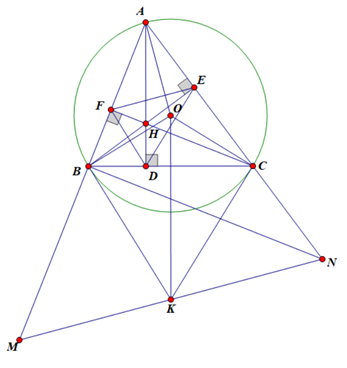
a)     Do AD, BE là các đường cao của \[\Delta ABC\]nên \[\Delta HDC\]vuông tại D

Do đó H, C, D cùng thuộc đường tròn đường kính HC.

Tương tự \[\Delta HEC\]vuông tại E nên H, C, E cùng thuộc đường tròn đường kính HC

Vậy H, E, C, D cùng thuộc đường tròn đường kính HC hay tứ giác CDHE nội tiếp đường tròn.

    b) Chứng minh tương tự câu a, ta có \[\Delta BEC\] vuông tại E và \[\Delta BFC\] vuông tại F nên B, C, E, F cùng thuộc đường tròn đường kính BC. Suy ra \[\widehat {EFC} = \widehat {EBC}\] (hai góc nội tiếp cùng chắn cung EC)

Do tứ giác EFCB nội tiếp nên \[\widehat {FEB} = \widehat {FCB}\] (hai góc nội tiếp cùng chắn cung FB)

Lại có \[\widehat {HED} = \widehat {HCD}\] (hai góc nội tiếp cùng chắn cung HD) nên \[\widehat {FEB} = \widehat {BED}\]

Kết hợp với \[\widehat {EFH} = \widehat {HBD}\] (hai góc nội tiếp cùng chắn cung CE) suy ra \[\Delta H{\rm{EF}} \sim \Delta {\rm{DEB(g}}{\rm{.g)}}\]

Suy ra \[\frac{{HE}}{{DE}} = \frac{{HF}}{{DB}}{\rm{ hay }}HE.{\rm{ }}DB{\rm{ }} = {\rm{ }}HF.{\rm{ }}DE\] (đpcm)

c) Ta có KB = KC (tính chất hai tiếp tuyến cắt nhau) và OB = OC (Cùng bằng bán kính của (O))

Suy ra OK là trung trực của đoạn thằng BC

Ta có: \[\widehat {OBK} = 90^\circ \] (do BK là tiếp tuyến) nên \[\widehat {MBK} + \widehat {OBA} = 180^\circ  - \widehat {OBK} = 90^\circ \]

Hay \[\widehat {MBK} = 90^\circ  - \widehat {OBA}{\rm{  (1)}}\]

Ta có \[\widehat {ACB} = \widehat {AFE}\] (do cùng cộng với \[\widehat {EFB}\] bằng \[180^\circ \]

Suy ra \[\widehat {OBA} = \widehat {OAB} = \frac{{180^\circ  - \widehat {AOB}}}{2} = 90^\circ  - \frac{{\widehat {AOB}}}{2} = 90^\circ  - \widehat {ACB} = 90^\circ  - \widehat {AFE}\]

Thay vào (1) suy ra \[\widehat {MBK} = 90^\circ  - \left( {90^\circ  - \widehat {AFE}} \right) = \widehat {AFE}\]

Mà \[\widehat {AFE} = \widehat {AMN}\] (vì là hai góc đồng vị) nên \[\widehat {MBK} = \widehat {BMK}\]hay \[\Delta MBK\]cân tại K

Suy ra MK = KB

Chứng minh tương tự ta được \[\Delta KCN\]cân tại K hay KC = KN

Vậy KM = KN = KB = KC hay M, N, C, B cùng thuộc một đường tròn đường kính MN

Suy ra \[\widehat {MBN} = 90^\circ \] (góc nội tiếp chắn nửa đường tròn)

Vậy \[AM \bot BN\]

Thể tích nước trong ly ban đầu là: \[{V_1} = \pi {R^2}h = \pi {.3^2}.5 = 45\pi (c{m^3})\]

Thể tích mỗi viên bi sắt là: \[{V_{bi}} = \frac{4}{3}\pi {r^3} = \frac{4}{3}\pi {.1^3} = \frac{4}{3}\pi (c{m^3})\]

Thể tích 6 viên bi sắt là: \[{V_2} = 6.\frac{4}{3}\pi = 8\pi (c{m^3})\]

Thể tích nước trong ly sau khi thả 6 viên bi sắt vào là: \[V = 45\pi + 8\pi = 53\pi (c{m^3})\]

Chiều cao mực nước trong ly sau khi thả 6 viên bi đó vào là: \[h' = \frac{V}{{\pi {R^2}}} = \frac{{53\pi }}{{\pi {{.3}^2}}} = \frac{{53}}{9} \approx 5,89(cm)\].