Cho biểu thức \[B = \frac{2}{{\sqrt {\rm{x}} + 2}} + \frac{3}{{\sqrt {\rm{x}} - 2}}\left( {{\rm{x}} \ge {\rm{0}}{\rm{,x}} \ne {\rm{4}}} \right)\]
a) Rút gọn biểu thức \(B\)
b) Tính giá trị của biểu thức \(B\) khi \({\rm{x}} = 9\).
Cho biểu thức \[B = \frac{2}{{\sqrt {\rm{x}} + 2}} + \frac{3}{{\sqrt {\rm{x}} - 2}}\left( {{\rm{x}} \ge {\rm{0}}{\rm{,x}} \ne {\rm{4}}} \right)\]
a) Rút gọn biểu thức \(B\)
b) Tính giá trị của biểu thức \(B\) khi \({\rm{x}} = 9\).Quảng cáo
Trả lời:
a) \(B = \frac{2}{{\sqrt {x + 2} }} + \frac{3}{{\sqrt {x - 2} }} = \frac{{2(\sqrt {x - 2} ) + 3(\sqrt {x + 2} )}}{{(\sqrt {x + 2} )(\sqrt {x - 2} )}} = \frac{{5\sqrt {x + 2} }}{{x - 4}}\)
b) với \(x = 9 \Rightarrow B = \frac{{5\sqrt 9 + 2}}{{9 - 4}} = \frac{{17}}{5}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
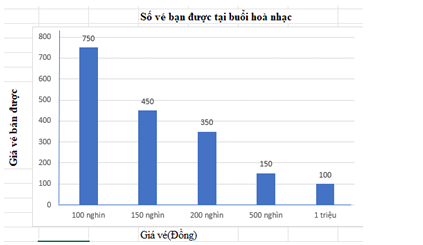
Tổng số tiền bán vé thu được là:
\[750\,\,100 + 450\,\,150 + 350\,\,200 + 150\,\,500 + 1\,\,001\,\,000 = 387\,\,500\] (nghìn đồng)
Lời giải
Không gian mẫu \(\Omega = \left\{ {1;2;3;4;5;6;7;8;9;10} \right\} \Rightarrow n\left( \Omega \right) = 10\)
- Biến cố thuận lợi \(A = \left\{ {1;2;3;4} \right\} \Rightarrow n\left( A \right) = 4\)
Vậy \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{4}{{10}} = \frac{2}{5}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.