Cho \(\Delta ABC\) vuông tại \(A\); \(AB = 10cm\); \(\widehat {ABC} = {60^0}\). Tính độ dài đoạn \(BC\), biết \[cos{60^0} = \frac{1}{2}\].
Quảng cáo
Trả lời:
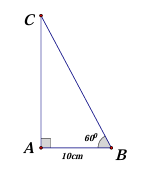
Áp dụng hệ thức lượng cho \(\Delta ABC\) vuông tại \(A\)ta có
\(\cos B = \frac{{AB}}{{BC}} \Rightarrow BC = \frac{{10}}{{\cos 60^\circ }} = 10.2 = 20\,\,({\rm{cm}})\)
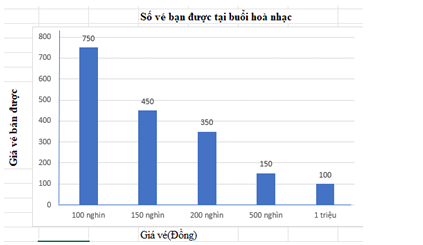
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Không gian mẫu \(\Omega = \left\{ {1;2;3;4;5;6;7;8;9;10} \right\} \Rightarrow n\left( \Omega \right) = 10\)
- Biến cố thuận lợi \(A = \left\{ {1;2;3;4} \right\} \Rightarrow n\left( A \right) = 4\)
Vậy \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{4}{{10}} = \frac{2}{5}\)
Lời giải
a) \(B = \frac{2}{{\sqrt {x + 2} }} + \frac{3}{{\sqrt {x - 2} }} = \frac{{2(\sqrt {x - 2} ) + 3(\sqrt {x + 2} )}}{{(\sqrt {x + 2} )(\sqrt {x - 2} )}} = \frac{{5\sqrt {x + 2} }}{{x - 4}}\)
b) với \(x = 9 \Rightarrow B = \frac{{5\sqrt 9 + 2}}{{9 - 4}} = \frac{{17}}{5}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.