Cho \(\Delta ABC\) đường cao \(AH\). Đường tròn \(\left( O \right)\) ngoại tiếp. Kẻ \(HD\) vuông góc với \(AB\), \(HE\) vuông góc với \(AC\) \(\left( {D \in AB,E \in AC} \right)\).

a) Chứng minh tứ giác \(ADHE\) nội tiếp.

b) Tính số đo \(\widehat {EDB}\), biết \(\widehat {ACB} = {40^0}\).

c) Đường thẳng qua \(E\) vuông góc với \(AB\) cắt tia \(AO\) tại \(M\). Chứng minh rằng \(DM \bot

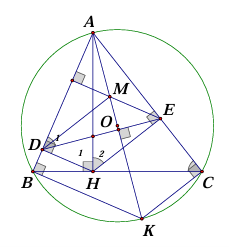
a) \(\Delta AHD\) vuông tại \(D\) nên \(A,D,H\) thuộc đường tròn đường kính \(AH\) (1)

\(\Delta AHE\) vuông tại \(E\) nên \(A,E,H\) thuộc đường tròn đường kính \(AH\) (2)

Từ (1) và (2) suy ra \(A,D,H,E\) thuộc đường tròn đường kính \(AH\),

hay \(ADHE\) nội tiếp.

b) Vì \(ADHE\) nội tiếp nên \(\widehat {{D_1}} = \widehat {{H_1}}\) (góc nội tiếp cùng chắn \(EC\))

 +) Vì \(\widehat {{H_1}} = \hat C\) (cùng phụ \(\widehat {{H_2}}\)) suy ra \(\hat C = \widehat {{D_1}} = 40^\circ \)

+) Vì \(\widehat {{D_1}} + \widehat {BDE} = 180^\circ \) (hai góc kề bù)

\( \Rightarrow \widehat {BDE} = 180^\circ  - 40^\circ  = 140^\circ \)

c) Kéo dài \(AO\) cắt \((O)\) tại điểm thứ hai \(K \Rightarrow \widehat {ABK} = \widehat {ACK} = 90^\circ \)

(góc nội tiếp chắn nửa đường tròn) và \(\widehat {KAC} = \widehat {KBC}\) (góc nội tiếp cùng chắn \(KC\))

+) Vì \(\widehat {KBC} = \widehat {BAH}\) (cùng phụ \(\widehat {ABH}\)) mà \(\widehat {BAH} + \widehat {DHA} = 90^\circ \)

+) Vì \(\widehat {DHA} = \widehat {DEA} \Rightarrow \widehat {KAC} + \widehat {DEA} = 90^\circ \) suy ra \(\Delta IAE\) vuông tại \(I\) (\(AK \cap DE = \{ I\} \))

\(AO\) là đường cao của tam giác \(\Delta ADE\) mà \(AM\) cũng là đường cao của \(\Delta ADE\) nên \(M\) là trực tâm của \(\Delta ADE\) nên \(DM \bot AE\).