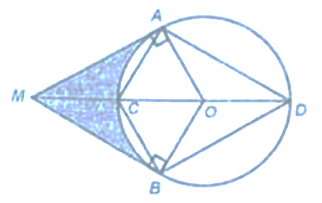
Cho đường tròn \(\left( {O;3cm} \right)\) và một điểm \(M\)nằm ngoài đường tròn sao cho \[OM = 6cm\]. Từ \(M\) vẽ các tiếp tuyến \(MA,MB\) của đường tròn \(\left( O \right)\), với \(A,B\) là các tiếp điểm; \(MO\) cắt đường tròn \(\left( O \right)\)tại hai điểm \(C\) và \(D\) (\(C\) thuộc cung nhỏ \(AB\))

Quảng cáo
Trả lời:
a) Vì các điểm \(A,B,C,D\) cùng nằm trên đường tròn nên tứ giác \(CADB\) là tứ giác nội tiếp. ĐÚNG
b) Vì \(B\)nằm trên đường tròn nên \(OB = 3cm\). ĐÚNG
c) Tam giác \(MAO\) vuông tại \(A\), đường trung tuyến \(AC\)(do \(MC = 3 = \frac{1}{2}MO\)) nên \(AC = \frac{1}{2}MO = 3cm\).
Suy ra tam giác \(AOC\) đều. do đó \(\widehat {AOC} = 60^\circ \). Suy ra \(\widehat {AOB} = 120^\circ \) (tính chất hai tiếp tuyến cắt nhau)
Suy ra \[\widehat {ADB} = \frac{1}{2}\widehat {AOB} = 60^\circ \]. SAI
d) Tam giác \(ADC\) vuông tại \(A\) (góc nội tiếp \(A\) chắn nửa đường tròn). Nên \(DC = CD.\cos \widehat {ADC} = 6.\frac{{\sqrt 3 }}{2} = 3\sqrt 3 cm\).
Tam giác \(ABD\) cân tại \[{\rm{D}}\] có \[\widehat D = 60^\circ \] nên tam giác đều. Do đó đường chéo \(AB = AD = 3\sqrt 3 cm\)
Diện tích tứ giác \(MAOB\) là: \(\frac{1}{2}.3\sqrt 3 .6 = 9\sqrt 3 \left( {c{m^2}} \right)\).
Diện tích hình quạt \(OAB\)là: \(\frac{{\pi .9.120^\circ }}{{360^\circ }} = 3\pi \) \((c{m^2})\)
Vậy diện tích của hình giới hạn bới hai tiếp tuyến \(MA,MB\) và cung nhỏ \(AB\) (phần tô đạm trong hình vẽ) bằng \(9\sqrt 3 - 3\pi = 3\left( {3\sqrt 3 - \pi } \right)\left( {c{m^2}} \right)\) ĐÚNG
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
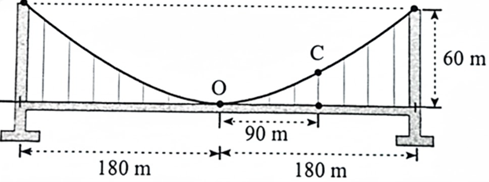
Gọi phương trình parabol: \(y = a{x^2}\) (\(a \ne 0\)).
Vì parabol đi qua điểm \(\left( {90;60} \right)\) nên \(a{.180^2} = 60 \Rightarrow a = \frac{{60}}{{180.180}} = \frac{1}{{540}}\).
Độ cao của dây cáp tại vị trí \(C\) (cách tâm \(O\) của mặt cầu \(90m\) theo phương ngang) so với mặt cầu là: \(y = \frac{1}{{540}}{.90^2} = 15\) (m)
Đáp số: \(15m\)
Lời giải
Xác suất lấy được viên bi xanh từ hộp thứ nhất là:\(\frac{1}{4}\)
Xác suất lấy được bi xanh từ hộp thứ hai là: \(\frac{3}{4}\)
Xác suất để lấy được hai viên bi màu xanh từ hai hộp là: \(\frac{1}{4}.\frac{3}{4} = \frac{3}{{16}}\).
Tương tự, xác suất để lấy được hai viên bi màu đỏ từ hai hộp là:
\(\frac{3}{4}.\frac{1}{4} = \frac{3}{{16}}\).
Do đó xác suất của biến cố “Hai viên bi bạn Dương lấy ra cùng màu” là:
\(\frac{3}{{16}} + \frac{3}{{16}} = \frac{6}{{16}} \approx 0,38\)
Đáp số: \(0,38\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.