Một bình đựng nước cam có dạng hình trụ với đường kính đáy \(20cm\). Phần nước cam bên trong bình cao \(24cm\). Người ta rót nước cam từ bình này vào các ly có hình dạng và kích thước giống nhau. Phần đựng được nước của chiếc ly có dạng hình nón với chiều cao \(7,5cm\) và đường kính đáy \(10cm\). Người ta rót nước cam vào mỗi ly sao cho chiều cao của khối nước cam bằng \(6cm\). Hỏi người đó có thể rót được bao nhiêu ly nước cam như vậy? Giải thiết độ dày của bình và ly không đáng kể.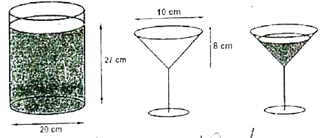
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án:
75
Thể tích nước cam là: \(\pi {.10^2}.24 = 2400\pi \left( {c{m^3}} \right)\)
Tỉ số bán kính đáy nhỏ của hình nón khi chiều cao mực nước là 6cm và bán kính của chiếc ly cao 7,5cm là: \(\frac{{{r_{nho}}}}{{{r_{lon}}}} = \frac{{{h_{nho}}}}{{{h_{lon}}}} = \frac{6}{{7,5}} = \frac{4}{5}\).
Bán kính hình nón nhỏ là: \(\frac{4}{5}.5 = 4\left( {cm} \right)\).
Thể tích nước cam trong một ly là: \(\frac{1}{3}\pi {.4^2}.6 = 32\pi \left( {c{m^3}} \right)\)
Số ly nước cam rót được là: \(\frac{{2400\pi }}{{32\pi }} = 75\) (ly).
Đáp số: \(75\) ly.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
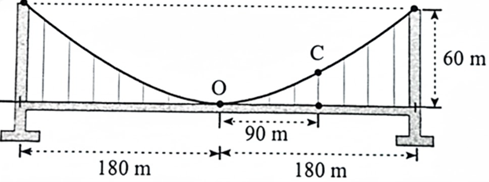
Gọi phương trình parabol: \(y = a{x^2}\) (\(a \ne 0\)).
Vì parabol đi qua điểm \(\left( {90;60} \right)\) nên \(a{.180^2} = 60 \Rightarrow a = \frac{{60}}{{180.180}} = \frac{1}{{540}}\).
Độ cao của dây cáp tại vị trí \(C\) (cách tâm \(O\) của mặt cầu \(90m\) theo phương ngang) so với mặt cầu là: \(y = \frac{1}{{540}}{.90^2} = 15\) (m)
Đáp số: \(15m\)
Lời giải
Chọn C
Câu 3
a) Tứ giác \(CADB\) là tứ giác nội tiếp.
Đúng
Sai
b) \(OB = 3cm\)
Đúng
Sai
c) \(\widehat {ADB} = 45^\circ \)
Đúng
Sai
d) Diện tích của hình giới hạn bới hai tiếp tuyến \(MA,MB\) và cung nhỏ \(AB\) (phần tô đạm trong hình vẽ) bằng \(3\left( {3\sqrt 3 - \pi } \right)c{m^2}\).
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(4x < 4y\).
B. \(x - y < 0\).
C. \( - x > - y\).
D. \(x - 3 > y - 3\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\frac{x}{y} = \frac{5}{7}\).
B. \(\frac{x}{5} = \frac{y}{7}\)
C. \(\frac{x}{5} = \frac{7}{y}\).
D. \(\frac{x}{7} = \frac{y}{5}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[12\]cm.
B. \[\frac{{160}}{3}\]cm.
C. \(32\)cm.
D. \(\frac{{100}}{3}\)cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập