Biết tích phân \[\int\limits_0^{\ln 2\sqrt 2 } {\frac{{{e^x}}}{{\sqrt {{e^{2x}} + 1} }}} \,{\rm{d}}x = \ln \left( {\sqrt a + b} \right)\], với \[a,\,b\] là số nguyên dương. Tính tích \[a \cdot b\].
Câu hỏi trong đề: Đề kiểm tra Tích phân (có lời giải) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án:
2
Đặt \[u = {e^x}\] ta có \[x = 0 \Rightarrow u = 1;\,x = \ln 2\sqrt 2 \Rightarrow u = 2\sqrt 2 \]; \[{\rm{d}}u = {e^x}{\rm{d}}x\]
Ta có \[\int\limits_0^{\ln 2\sqrt 2 } {\frac{{{e^x}}}{{\sqrt {{e^{2x}} + 1} }}} \,{\rm{d}}x = \int\limits_1^{2\sqrt 2 } {\frac{{{\rm{d}}u}}{{\sqrt {{u^2} + 1} }}} \]
Đặt \[t = u + \sqrt {{u^2} + 1} \Rightarrow {\rm{d}}t = \left( {1 + \frac{u}{{\sqrt {{u^2} + 1} }}} \right){\rm{d}}u \Rightarrow {\rm{d}}t = \frac{{u + \sqrt {{u^2} + 1} }}{{\sqrt {{u^2} + 1} }}{\rm{d}}u \Leftrightarrow \frac{{{\rm{d}}t}}{t} = \frac{{{\rm{d}}u}}{{\sqrt {{u^2} + 1} }}\]
Đổi cận \[u = 1 \Rightarrow t = 1 + \sqrt 2 ;\,u = 2\sqrt 2 \Rightarrow t = 3 + 2\sqrt 2 \]
\[\int\limits_1^{2\sqrt 2 } {\frac{{{\rm{d}}u}}{{\sqrt {{u^2} + 1} }}} = \int\limits_{1 + \sqrt 2 }^{3 + 2\sqrt 2 } {\frac{{{\rm{d}}t}}{t}} = \left. {\ln \left| t \right|} \right|_{1 + \sqrt 2 }^{3 + 2\sqrt 2 } = \ln \left( {1 + \sqrt 2 } \right)\]
Ta có \[a = 2,\,b = 1 \Rightarrow a \cdot b = 2\]Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Các sản phẩm khác của Vietjack:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Vận tốc của vật được biểu diển bởi hàm số \(v\left( t \right) = \int {a\left( t \right) = \int {10\sin t{\rm{d}}t} } = - 10\cos t + C\).
Khi vật bắt đầu chuyển động, vật có vận tốc là \(5{\rm{ m/s}}\) nên ta có \(v\left( 0 \right) = 5 \Leftrightarrow - 10\cos 0 + C = 5 \Leftrightarrow C = 15\).
Do đó \(v\left( t \right) = - 10\cos t + 15\).
Ta có \( - 1 \le \cos t \le 1,{\rm{ }}\forall t \in \left[ {0;\pi } \right]\)
\( \Leftrightarrow 10 \ge - 10\cos t \ge - 10,{\rm{ }}\forall t \in \left[ {0;\pi } \right]\)
\[ \Leftrightarrow 25 \ge - 10\cos t + 15 \ge 5,{\rm{ }}\forall t \in \left[ {0;\pi } \right]\]
\( \Leftrightarrow 25 \ge v\left( t \right) \ge 5,{\rm{ }}\forall t \in \left[ {0;\pi } \right]\)
Vậy vận tốc của vật đạt giá trị lớn nhất là \(25{\rm{ m/s}}\) khi \(t = \pi \).
Khi đó, gia tốc của vật tại thời điểm \(t = \pi \) là \(a\left( \pi \right) = 10\sin \pi = 0{\rm{ }}\left( {{\rm{m/s}}} \right)\).Lời giải
\[\int\limits_1^2 {\left( {\frac{{{x^2} + 1}}{x}} \right)} \,{\rm{d}}x = \int\limits_1^2 {\left( {x + \frac{1}{x}} \right)} \,{\rm{d}}x = \left. {\left( {\frac{{{x^2}}}{2} + \ln \left| x \right|} \right)} \right|_1^2 = \ln 2 + \frac{3}{2} = \ln a + \frac{b}{c} \Rightarrow a = 2,\,b = 3,\,c = 2\]
\[ \Rightarrow a + b + c = 7\].Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
a) Diện tích hình phẳng giới hạn bởi đồ thị \[\left( P \right)\], \[Ox\] và 2 đường thẳng \[x = 0,\,\,x = 1\] bằng \[\frac{{38}}{3}\].
Đúng
Sai
b) Diện tích hình phẳng giới hạn bởi đồ thị \[\left( P \right)\], đường thẳng \[\Delta :y = 2025\] và 2 đường thẳng \[x = 0,\,\,x = 1\] bằng diện tích hình phẳng giới hạn bởi đồ thị \[\left( P \right)\], đường thẳng \[\Delta :y = 2025\] và 2 đường thẳng \[x = - 1,\,\,x = 0\] .
Đúng
Sai
c) Diện tích hình phẳng giới hạn bởi đồ thị \[\left( P \right)\] và \[Ox\] xấp xỉ bằng 38.
Đúng
Sai
d) Diện tích hình phẳng giới hạn bởi đồ thị \[\left( P \right)\] và \[Ox\] gấp 3 lần diện tích hình phẳng giới hạn bởi đồ thị \[\left( P \right)\], \[Ox\] và 2 đường thẳng \[x = 0,\,\,x = \frac{{\sqrt {14} }}{2}\] .
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
a) \(\int\limits_1^2 {{x^2}} = \frac{7}{3}\).
Đúng
Sai
b) Nếu \(m\) là tham số, tích phân \(\int\limits_0^2 {\left( {4{x^3} + m} \right){\rm{d}}x} = 4\) thì \(m = - \,4\).
Đúng
Sai
c) Cho biết \(m,\,n,\,p\) là các số thực. Tích phân \(\int\limits_1^2 {\left( {\pi {x^5} + e{x^2} + 1} \right){\rm{d}}x} = m\pi + ne + p\). Giá trị của \(2m - 3n + p\) bằng \(15\).
Đúng
Sai
d) Cho hàm số \(y = f\left( x \right)\) là hàm số bậc hai có đồ thị như hình vẽ.
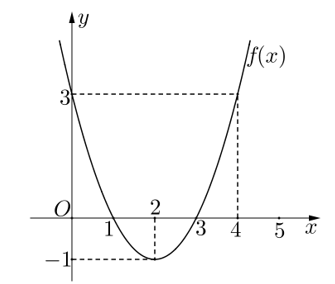
Tích phân \(\int\limits_0^1 {f\left( x \right){\rm{d}}x} + \int\limits_3^5 {f\left( x \right){\rm{d}}x} \) bằng \(10\).
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
a) \(\int\limits_a^b {f\left( x \right){\rm{d}}x} = F\left( b \right) - F\left( a \right)\).
Đúng
Sai
b) \(\int\limits_b^a {f\left( x \right){\rm{d}}x} = - \,\int\limits_a^b {f\left( x \right){\rm{d}}x} \).
Đúng
Sai
c) Nếu \(a < c < b\) và \(\int\limits_a^b {f\left( x \right){\rm{d}}x} = m,\,\,\int\limits_c^a {f\left( x \right){\rm{d}}x} = n\) thì \(\int\limits_c^b {f\left( x \right){\rm{d}}x} = m - n\).
Đúng
Sai
d) \[\int\limits_a^b {\left[ {2024f\left( x \right) + 2025} \right]{\rm{d}}x} = 2024\int\limits_a^b {f\left( x \right){\rm{d}}x} + 2025\left( {a - b} \right)\].
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập