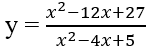Câu hỏi trong đề: Giải sbt Giải tích 12 Bài 4: Đường tiệm cận !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Vì
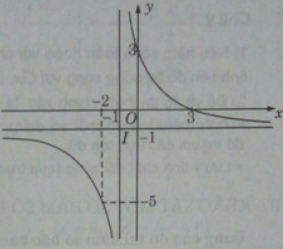
nên x = 1 là tiệm cận đứng.
Từ
Suy ra y = 1 là tiệm cận ngang.
b) Vì
và
nên x = 2 là một tiệm cận đứng.
Do
và
nên x = -2 là tiệm cận đứng thứ hai.
Ta lại có
nên y = a là tiệm cận ngang.
c) Do
nên x = 1 là tiệm cận đứng.
Mặt khác,
nên x = 3 cũng là tiệm cận đứng.
Vì
nên y = 0 là tiệm cận ngang.
d) TXĐ: R.
Từ
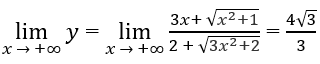
Ruy ra đồ thị hàm số có các tiệm cận ngang:
Đồ thị hàm số không có tiệm cận đứng.
e) TXĐ: D = (-∞; -√2) ∪ (√2;4) ∪ (4; +∞)
Do
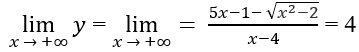
Cho nên đồ thị hàm số có hai tiệm cận ngang
y = 4 khi x ⇒ +∞
y = 6 khi x ⇒ -∞
Vì
Cho nên đường thẳng x = 4 là tiệm cận đứng của đồ thị hàm số.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: D.
Tiệm cận đứng của đồ thị hàm số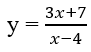 
là x = 4; tiệm cận ngang của đồ thị hàm số đó là y = 3. Diện tích hình chữ nhật tạo thành là 3 x 4 = 12.
Lời giải
a) Ta có:
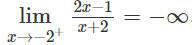
nên đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.
Vì
nên đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.
b) Từ
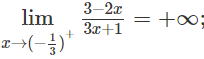
ta có x = −1/3 là tiệm cận đứng
Vì
nên đường thẳng y = -2/3 là tiệm cận ngang.
c) Vì
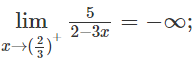
nên x = 2/3 là tiệm cận đứng.
Do
nên y = 0 là tiệm cận ngang.
d) Do
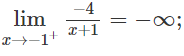
nên x = -1 là tiệm cận đứng.
Vì
nên y = 0 là tiệm cận ngang.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
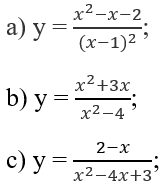
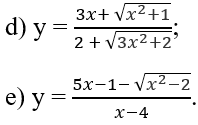
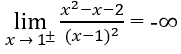
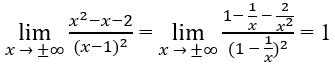
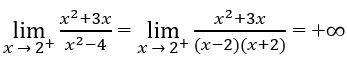
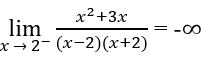
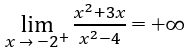
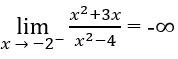
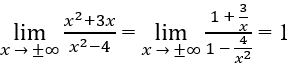
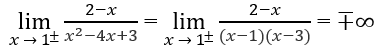
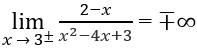
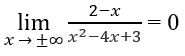
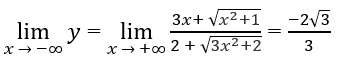
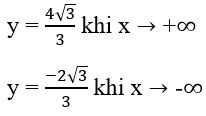
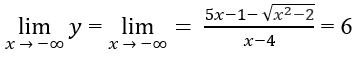
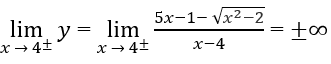
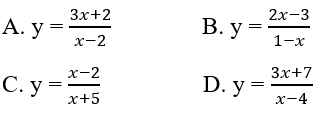
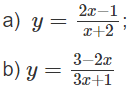
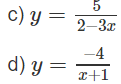
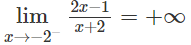
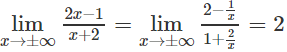
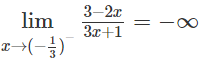
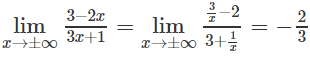
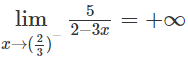
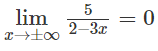
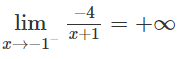
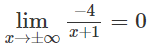
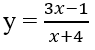
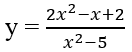
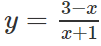có đồ thị (H)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)