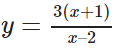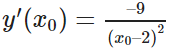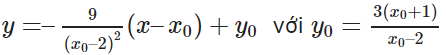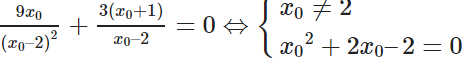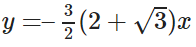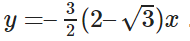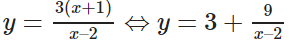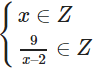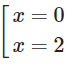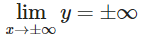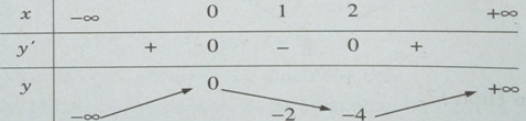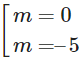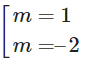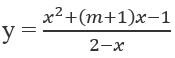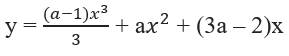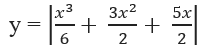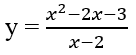Cho hàm số:
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
b) Viết phương trình các đường thẳng đi qua O(0;0) và tiếp xúc với (C) .
c) Tìm tất cả các điểm trên (C) có tọa độ là các số nguyên.
Câu hỏi trong đề: Giải sbt Giải tích 12 Bài tập ôn tập chương 1 !!
Quảng cáo
Trả lời:
a) Học sinh tự làm
b) Phương trình tiếp tuyến tại điểm M0(x0; y0) là:
y – y0 = y’(x0)(x – x0)
Trong đó:
Ta có:
Để đường thẳng đó đi qua O(0; 0), điều kiện cần và đủ là:
⇔ x0 = –1 - hoặc x0 = –1 +
+) Với x0 = –1 + , ta có phương trình tiếp tuyến:
+) Với x0 = –1 – , ta có phương trình tiếp tuyến:
c) Để tìm trên (C) các điểm có tọa độ nguyên ta có:
Điều kiện cần và đủ để M(x, y) ∈ (C) có tọa độ nguyên là:
tức (x – 2) là ước của 9.
Khi đó, x – 2 nhận các giá trị -1; 1; -3; 3; -9; 9 hay x nhận các giá trị 1; 3; -1; 5; -7; 11.
Do đó, ta có 6 điểm trên (C) có tọa độ nguyên là: (1;-6), (3;12), (-1;0), (5;6), (-7;2), (11;4).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) TXĐ: D = R
Sự biến thiên:
y′ = 3 – 6x = 3x(x – 2)
y′=0 ⇔
Hàm số đồng biến trên mỗi khoảng (–;0), (2;+)
Hàm số nghịch biến trên khoảng (0; 2).
Hàm số đạt cực đại tại x = 0 ; = y(0) = 0
Hàm số đạt cực tiểu tại x = 2; = y(2) = -4.
Giới hạn:
Điểm uốn: y” = 6x – 6, y” = 0 ⇔ x = 1; y(1) = –2
Suy ra đồ thị có điểm uốn I(1; -2)
Bảng biến thiên:
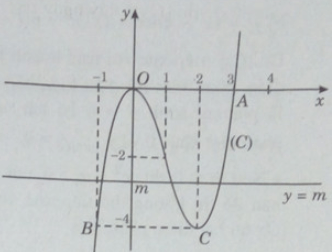
Đồ thị:
Đồ thị cắt trục hoành tại O(0;0), A(3;0). Đồ thị đi qua điểm B(-1;-4); C(2;-4).
b) – 3 – m = 0 ⇔ – 3 = m – 3 – m = 0 ⇔ – 3 = m (∗)
Phương trình (∗) có 3 nghiệm phân biệt khi và chỉ khi đường thẳng y = m cắt (C) tại 3 điểm phân biệt. Từ đó suy ra: – 4 < m < 0.
Lời giải
a) y = –( + 5m) + 6m + 6x – 5
y′ = –3( + 5m) + 12mx + 6
Hàm số đơn điệu trên R khi và chỉ khi y’ không đổi dấu.
Ta xét các trường hợp:
+) m2 + 5m = 0 ⇔
– Với m = 0 thì y’ = 6 nên hàm số luôn đồng biến.
– Với m = -5 thì y’ = -60x + 6 đổi dấu khi x đi qua .
+) Với + 5m ≠ 0. Khi đó, y’ không đổi dấu nếu
Δ' = 36 + 18( + 5m) ≤ 0 ⇔ 3 + 5m ≤ 0 ⇔ –5/3 ≤ m ≤ 0
– Với điều kiện đó, ta có –3( + 5m) > 0 nên y’ > 0 và do đó hàm số đồng biến trên R.
Vậy với điều kiện –5/3 ≤ m ≤ 0 thì hàm số đồng biến trên R.
b) Nếu hàm số đạt cực đại tại x = 1 thì y’(1) = 0. Khi đó:
y′(1) = –3 – 3m + 6 = 0 ⇔
Mặt khác, y” = –6( + 5m)x + 12m
+) Với m = 1 thì y’’ = -36x + 12. Khi đó, y’’(1) = -24 < 0 , hàm số đạt cực đại tại x = 1.
+) Với m = -2 thì y’’ = 36x – 24. Khi đó, y’’(1) = 12 > 0, hàm số đạt cực tiểu tại x = 1.
Vậy với m = 1 thì hàm số đạt cực đại tại x = 1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.