Vẽ đoạn thẳng BC = 3 cm. Vẽ hai tia Bx và Cy sao cho như Hình 4.33. Lấy giao điểm A của hai tia Bx và Cy, ta được tam giác ABC (H.4.33). Dùng thước thẳng có vạch chia đo độ dài hai cạnh AB, AC của tam giác ABC.
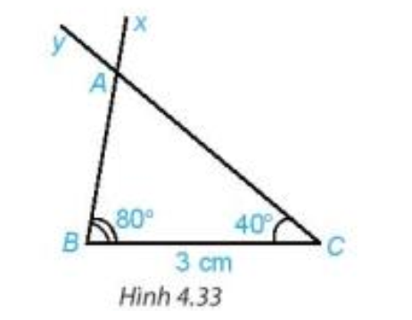
Vẽ đoạn thẳng BC = 3 cm. Vẽ hai tia Bx và Cy sao cho như Hình 4.33. Lấy giao điểm A của hai tia Bx và Cy, ta được tam giác ABC (H.4.33). Dùng thước thẳng có vạch chia đo độ dài hai cạnh AB, AC của tam giác ABC.
Quảng cáo
Trả lời:
Tương tự Hoạt động 3, ta vẽ hình như sau:
Bước 1. Vẽ đoạn thẳng B'C'=3 cm
Bước 2. Dùng thước đo độ, vẽ hai tia B'x' và C'y' sao cho
Bước 3. Lấy giao điểm A' của hai tia B'x' và C'y' ta được tam giác A'B'C'
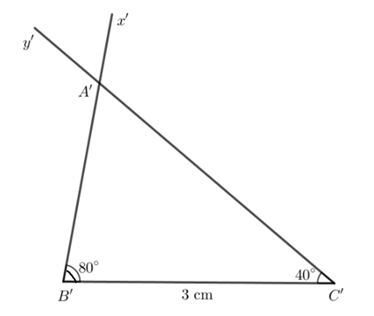
- Dùng thước thẳng có vạch chia, ta đo được và BC=B'C'=3 cm
- Xét hai tam giác ABC và A'B'C' có:
AB=A'B' (chứng minh trên).
(cùng bằng 80o).
BC = B'C' (chứng minh trên).
Vậy (c – g – c).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Xét hai tam giác AOD và COB có:
OA = OC (theo giả thiết).
(2 góc đối đỉnh).
OD = OB (theo giả thiết).
Vậy (c – g – c).
Xét hai tam giác AOB và COD có:
OA = OC (theo giả thiết).
(2 góc đối đỉnh).
OB = OD (theo giả thiết).
Vậy (c – g – c).
b) Do nên AD = BC (2 cạnh tương ứng).
Do nên AB = CD (2 cạnh tương ứng).
Xét hai tam giác DAB và BCD có:
AD = BC (chứng minh trên).
AB = CD (chứng minh trên).
BD chung.
Vậy (c – c – c).
Lời giải
a) Do AB = CD nên AB + BC = CD + BC.
hay AC = DB.
Vậy AC = DB.
b) Xét hai tam giác OAC và ODB có:
OA = OD (theo giả thiết).
(theo giả thiết).
AC = BD (chứng minh trên).
Vậy (c – g – c).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.