Trong không gian Oxyz, cho đường thẳng và hai điểm A(3;2;1), B(2;0;4). Gọi là đường thẳng qua A, vuông góc với d sao cho khoảng cách từ B đến là nhỏ nhất. Gọi =(2;b;c) là một VTCP của . Khi đó, bằng
A.
B.
C.
D. 3
Quảng cáo
Trả lời:
Đáp án B
Cách giải:
![]()
có 1 VTCP =(1;-2;2) là một VTCP của
là đường thẳng qua A, vuông góc với d mặt phẳng qua A và vuông góc d mặt phẳng qua A và vuông góc d
Phương trình mặt phẳng
![]()
![]()
![]()
khi và chỉ khi đi qua hình chiếu H của B lên
*) Tìm tọa độ điểm H:
Đường thẳng BH đi qua B(2;0;4) và có VTCP là VTPT của có phương trình:
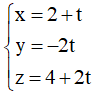
![]()
![]()
![]()
![]()
![]()
![]()
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 2y+3z-10=0
B.2x+3z-11=0
C. 2y+3z-12=0
D. 2y+3z-11=0
Lời giải
Đáp án D
Ta có:
![]()
Khi đó:
![]()
Suy ra (Q): 2y+3z-11=0
Câu 2
A. 3x+y-2z-2=0
B. 3x-2z=0
C. 3x-2z-1=0
D. 3x-y+2z-4=0
Lời giải
Đáp án C
Phương pháp
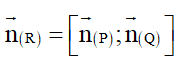
Cách giải: Ta có:
![]()
![]()
là 1 VTPT của mặt phẳng (R).
Vậy phương trình mặt phẳng (R):
![]()
Câu 3
A. (Q): 2y+z=0
B. (Q): 2x-z=0
C. (Q): y-2z=0
D. (Q): 2y-z=0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. x+2y+4z+1=0
B. 4x+2y+z-8=0
C. 2x-y-z-1=0
D. 4x+2y+z+1=0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.