Có 4 quyển sách Toán, 6 quyển sách Lý và 8 quyển sách Hóa khác nhau được xếp lên giá sách theo một hàng ngang. Tính xác suất để không có bất kỳ hai quyển sách Hóa đứng cạnh nhau.
Quảng cáo
Trả lời:
Chọn D
Gọi là không gian mẫu. Ta có: n() = 18!.
Gọi A là biến cố: “Xếp 18 quyển sách lên giá sách theo một hàng ngang sao cho không có bất kỳ hai quyển sách Hóa đứng cạnh nhau”.
![]() Xếp ngẫu nhiên 10 quyển sách gồm 4 quyển sách Toán và 6 quyển sách Lý vào 10 vị trí có 10! cách.
Xếp ngẫu nhiên 10 quyển sách gồm 4 quyển sách Toán và 6 quyển sách Lý vào 10 vị trí có 10! cách.
![]() Xếp 8 quyển sách Hóa vào 9 khoảng trống giữa 10 quyển sách Toán và Lý, vị trí đầu và cuối giá sách có cách.
Xếp 8 quyển sách Hóa vào 9 khoảng trống giữa 10 quyển sách Toán và Lý, vị trí đầu và cuối giá sách có cách.
=> n(A) = 10!.
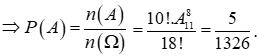
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 108864
B. 80640
C. 145152
D. 217728
Lời giải
Chọn C
Để xếp 9 em học sinh thành một hàng dọc ta thực hiện ba hành động liên tiếp
* Sắp xếp 3 học sinh lớp B. Có 3! cách.
* Sắp xếp 2 học sinh lớp A đứng cạnh các học sinh lớp B sao cho giữa hai học sinh lớp A không có học sinh lớp B. Có .2! cách.
* Lần lượt sắp xếp 4 học sinh lớp C còn lại đứng cạnh các học sinh trên. Có cách.
Vậy có tất cả 3!.2!.
Bình luận: Trong đề thi thử THPT chuyên Thái Nguyên lần 2 trong câu hỏi này không có đáp án 145152 mà thay bởi đáp án 145112. Tôi thiết nghĩ lỗi do người làm đề đã đánh máy nên đã tự ý đổi lại một đáp án khác mà tôi nghĩ chính xác hơn.
Lời giải
Chọn C
Số cách xếp 9 quyển sách lên một kệ sách dài là 9! . Suy ra số phần tử không gian mẫu: = 9!
Gọi A là biến cố: “các quyển sách cùng một môn nằm cạnh nhau”.
Ta xếp các cuốn sách cùng một bộ môn thành một nhóm
Trước hết ta xếp 2 nhóm lên kệ sách chúng ta có: 2! cách xếp
Với mỗi cách xếp 2 nhóm đó lên kệ ta có 5! cách hoán vị các cuốn sách Toán và 4! cách hoán vị các cuốn sách Văn. Suy ra n(A) = 5!.4!.2!
Xác suất cần tìm là 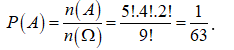
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.