Người ta sắp xếp ngẫu nhiên 5 viên bi được đánh số từ 1 đến 5 vào năm chiếc hộp theo một hàng ngang. Tính xác suất để các viên bi được đánh số chẵn luôn đứng cạnh nhau.
Quảng cáo
Trả lời:
Chọn B
Gọi là không gian mẫu. Ta có: n() = 5!.
Gọi A là biến cố: “Xếp 5 viên bi được đánh số từ 1 đến 5 vào năm chiếc hộp sao cho các viên bi được đánh số chẵn nằm trong các hộp đứng cạnh nhau ”.
![]() Xếp 2 viên bi có đánh số chẵn (viên bi số 2 và viên bi số 4) vào 2 hộp đứng cạnh nhau có 2! cách.
Xếp 2 viên bi có đánh số chẵn (viên bi số 2 và viên bi số 4) vào 2 hộp đứng cạnh nhau có 2! cách.
![]() Ta coi việc xếp 2 viên bi chẵn vào hai chiếc hộp đứng cạnh nhau là xếp chúng vào một chiếc hộp lớn.
Ta coi việc xếp 2 viên bi chẵn vào hai chiếc hộp đứng cạnh nhau là xếp chúng vào một chiếc hộp lớn.
![]() Xếp 3 viên bi có đánh số lẻ (viên bi số 1, viên bi số 3 và viên bi số 5) vào 3 chiếc hộp và 2 viên bi đánh số chẵn (viên bi số 2 và viên bi số 4) vào 1 chiếc hộp lớn nên ta có 4 chiếc hộp để sắp xếp, vậy có 4! cách.
Xếp 3 viên bi có đánh số lẻ (viên bi số 1, viên bi số 3 và viên bi số 5) vào 3 chiếc hộp và 2 viên bi đánh số chẵn (viên bi số 2 và viên bi số 4) vào 1 chiếc hộp lớn nên ta có 4 chiếc hộp để sắp xếp, vậy có 4! cách.
Vậy n(A) = 2!.4!
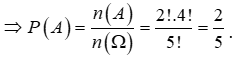
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 108864
B. 80640
C. 145152
D. 217728
Lời giải
Chọn C
Để xếp 9 em học sinh thành một hàng dọc ta thực hiện ba hành động liên tiếp
* Sắp xếp 3 học sinh lớp B. Có 3! cách.
* Sắp xếp 2 học sinh lớp A đứng cạnh các học sinh lớp B sao cho giữa hai học sinh lớp A không có học sinh lớp B. Có .2! cách.
* Lần lượt sắp xếp 4 học sinh lớp C còn lại đứng cạnh các học sinh trên. Có cách.
Vậy có tất cả 3!.2!.
Bình luận: Trong đề thi thử THPT chuyên Thái Nguyên lần 2 trong câu hỏi này không có đáp án 145152 mà thay bởi đáp án 145112. Tôi thiết nghĩ lỗi do người làm đề đã đánh máy nên đã tự ý đổi lại một đáp án khác mà tôi nghĩ chính xác hơn.
Lời giải
Chọn C
Số cách xếp 9 quyển sách lên một kệ sách dài là 9! . Suy ra số phần tử không gian mẫu: = 9!
Gọi A là biến cố: “các quyển sách cùng một môn nằm cạnh nhau”.
Ta xếp các cuốn sách cùng một bộ môn thành một nhóm
Trước hết ta xếp 2 nhóm lên kệ sách chúng ta có: 2! cách xếp
Với mỗi cách xếp 2 nhóm đó lên kệ ta có 5! cách hoán vị các cuốn sách Toán và 4! cách hoán vị các cuốn sách Văn. Suy ra n(A) = 5!.4!.2!
Xác suất cần tìm là 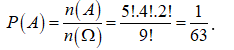
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.