Đề thi cuối học kỳ 2 Toán 6 Kết nối tri thức cấu trúc mới có đáp án - Đề 6

a) \(\frac{2}{5} - \frac{1}{5} \cdot \frac{3}{{ - 4}}\)

\( = \frac{2}{5} - \frac{3}{{ - 20}}\)

\( = \frac{8}{{20}} + \frac{3}{{20}}\)

\( = \frac{{11}}{{20}}.\)

c) \(\frac{2}{{11}}.\frac{{ - 5}}{4} + \frac{{ - 9}}{{11}}.\frac{5}{4} + 1\frac{3}{4}\)

\( = \frac{2}{{11}} \cdot \frac{{ - 5}}{4} + \frac{9}{{11}} \cdot \frac{{ - 5}}{4} + \frac{7}{4}\)

\( = \frac{{ - 5}}{4} \cdot \left( {\frac{2}{{11}} + \frac{9}{{11}}} \right) + \frac{7}{4}\)

\( = \frac{{ - 5}}{4} \cdot \frac{{11}}{{11}} + \frac{7}{4}\)

\( = \frac{{ - 5}}{4} \cdot 1 + \frac{7}{4}\)

\[ = \frac{{ - 5}}{4} + \frac{7}{4}\]

a) \(\frac{9}{{12}} - x = - \frac{3}{5}\)

\(x = \frac{9}{{12}} - \left( { - \frac{3}{5}} \right)\)

\(x = \frac{3}{4} + \frac{3}{5}\)

\(x = \frac{{27}}{{20}}\)

a) Số học sinh đạt loại Giỏi của lớp 6A là:

\(40 \cdot 25\% = 10\) (học sinh).

Số học sinh xếp loại Trung bình của lớp 6A là:

\(\frac{2}{5} \cdot 10 = 4\) (học sinh).

b) Số học sinh xếp loại Khá của lớp 6A là:

\(40 - 10 - 4 = 26\) (học sinh).

Tỉ số phần trăm số học sinh Khá so với số học sinh cả lớp là:

            \(\frac{{26}}{{40}} \cdot 100\% = 65\% \).

1)

a) Ta có: \(Oa\) và \(Ob\) là hai tia đối nhau

Mà \(M\) thuộc tia \(Oa\), \(N\) thuộc tia \(Ob\) nên \(OM\) và \(ON\) là hai tia đối nhau

Do đó điểm \(O\) nằm giữa hai điểm \(M\) và \(N.\)

b) Vì \(O\) nằm giữa hai điểm \(M\) và \(N\) nên \(MN = OM + ON\)

Suy ra \[MN = 5 + 3 = 8{\rm{\;(cm)}}{\rm{.}}\]

c) Trên tia \(MO\) ta có \(MP < MO\) (do \(2,5\,\,{\rm{cm}} < 5\,\,{\rm{cm)}}\)

Do đó \(P\) là điểm nằm giữa hai điểm \(M,O\)

Nên \(MO = MP + PO\)

Suy ra \(PO = MO - MP = 5 - 2,5 = 2,5{\rm{\;(cm)}}{\rm{.}}\)

Ta có: điểm \(P\) nằm giữa hai điểm \(M,O\) và \(MP = PO\,\,\left( { = 2,5\,\,{\rm{cm}}} \right)\) nên điểm \(P\) là trung điểm của đoạn thẳng \(OM.\)

2) a) Ta có \(15^\circ < 20^\circ < 25^\circ < 30^\circ \) nên \[\widehat {yOz} < \widehat {xOy} < \widehat {tOu} < \widehat {zOt}.\]

Do đó ta sắp xếp được các góc đã cho theo thứ tự số đo tăng dần như sau: \[\widehat {yOz},\,\,\widehat {xOy},\,\,\widehat {tOu},\,\,\widehat {zOt}.\]

Ta thấy các góc trên đều có số đo lớn hơn \(0^\circ \) và nhỏ hơn \(90^\circ \) nên các góc này đều là góc nhọn.

b) Ta có: \(\widehat {xOu} = \widehat {xOy} + \widehat {yOz} + \widehat {zOt} + \widehat {tOu} = 20^\circ + 15^\circ + 30^\circ + 25^\circ = 90^\circ \)

Do đó góc \(xOu\) là góc vuông.

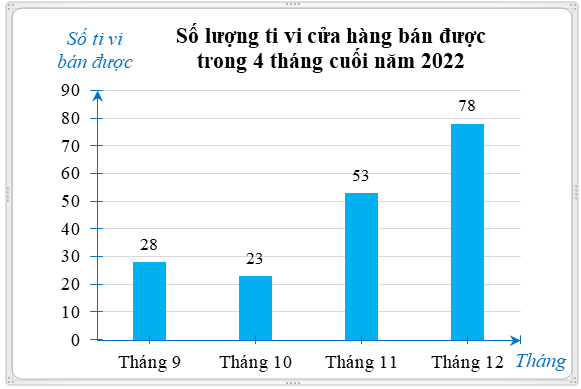
1) a) Biểu đồ đã cho cho biết thông tin số lượng ti vi cửa hàng bán được trong 4 tháng cuối năm 2022.

b) Tháng 12 cửa hàng bán được nhiều ti vi nhất.

Tháng 9 cửa hàng bán được ít ti vi nhất.

Tháng 12 bán được nhiều hơn tháng 9 bán được số chiếc ti vi là:

\(78 - 28 = 50\) (chiếc).

c) Theo em, sự kiện Giải bóng đá World Cup 2022 có liên quan đến việc mua bán ti vi trong tháng 11 và tháng 12, có thể vì nhu cầu xem bóng đá trên ti vi tăng cao.

2) Số lần cả hai đồng xu cùng xuất hiện mặt ngửa là: \(50 - 26 - 14 = 10\) (lần).

Hai đồng xu xuất hiện mặt giống nhau tức là cùng sấp hoặc cùng ngửa.

Vậy xác suất thực nghiệm của sự kiện xuất hiện hai đồng xu giống nhau là: \(\frac{{10 + 14}}{{50}} = \frac{{24}}{{50}} = \frac{{12}}{{25}}.\)