Bộ 5 đề thi cuối kì 1 Toán 6 Kết nối tri thức cấu trúc mới có đáp án - Đề 4
12 người thi tuần này 4.6 65 lượt thi 5 câu hỏi 60 phút
🔥 Đề thi HOT:
Dạng 4: Một số bài tập nâng cao về lũy thừa
15.9 K lượt thi
10 câu hỏi
31 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án
12.2 K lượt thi
31 câu hỏi
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 1)
10.8 K lượt thi
40 câu hỏi
10 câu Trắc nghiệm Toán 6 Chân trời sáng tạo Bài 1: Tập hợp. Phần tử của tập hợp (có đáp án)
4.9 K lượt thi
10 câu hỏi
Dạng 1. Biểu diễn một tập hợp cho trước
5.3 K lượt thi
45 câu hỏi
Dạng 1: Thực hiện tính, viết dưới dạng lũy thừa
14.9 K lượt thi
45 câu hỏi
20 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án (Phần 2)
3.8 K lượt thi
19 câu hỏi
5 câu Trắc nghiệm Toán 6 Cánh diều Bài 1: Tập hợp có đáp án ( Nhận biết )
5 K lượt thi
5 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải
|
a) \({3.5^2} - 16:{2^2}\) \[ = 3.25 - 16:4\] \[ = 75 - 4\] \( = 71\). |
b) \[\left( {1\,\,267 - 196} \right) - \left( {267 + 304} \right)\] \[ = 1\,\,267 - 196 - 267 - 304\] \[ = \left( {1\,\,267 - 267} \right) - \left( {196 + 304} \right)\] \[ = 1\,\,000 - 500\] \[ = 500\]. |
c) \[25 \cdot 75 - 3 \cdot 70 + 25 \cdot 125 - 3 \cdot 130\] \[ = \left( {25 \cdot 75 + 25 \cdot 125} \right) - \left( {3 \cdot 70 + 3 \cdot 130} \right)\] \[ = 25 \cdot \left( {75 + 125} \right) - 3 \cdot \left( {70 + 130} \right)\] \[ = 25 \cdot 200 - 3 \cdot 200\] \[ = 200 \cdot \left( {25 - 3} \right)\] \[ = 200 \cdot 22\] \[ = 4\,\,400\]. |
Lời giải
Hướng dẫn giải
|
1. a) \(9 \cdot \left( {x + 2} \right) - 28 = 26\) \(9 \cdot \left( {x + 2} \right) = 54\) \(x + 2 = 6\) \(x = 4\) Vậy \(x = 4.\) |
1. b) \(\left( { - 6 + 3x} \right):5 = - 18\) \( - 6 + 3x = - 90\) \(3x = - 84\) \(x = - 28\). Vậy \(x = - 28\). |
1. c) \({\left( {4 - x} \right)^3} + 17 = - 10\) \({\left( {4 - x} \right)^3} = - 27\) \({\left( {4 - x} \right)^3} = {\left( { - 3} \right)^3}\) Suy ra \(4 - x = - 3\) \(x = 4 - \left( { - 3} \right)\) \(x = 7\) Vậy \(x = 7.\) |
2. Ta có Ư\(\left( {100} \right) = \left\{ {1\,;\,\,2\,;\,\,4\,;\,\,5\,;\,\,10\,;\,\,20\,;\,\,25\,;\,\,50\,;\,\,100} \right\}.\)
Vì \(x \in B\left( {25} \right)\) nên \(x\,\, \vdots \,\,25.\)
Do đó \(x \in \left\{ {25\,;\,\,50\,;\,\,100} \right\}.\)
Câu 3
(3,0 điểm)
1. “Nhà Tây Sơn là một triều đại quan chủ trong lịch sử Việt Nam tồn tại từ năm 1778 đến năm 1802. Theo cách gọi của phần lớn sử gia tại Việt Nam thì “nhà Tây Sơn” được dùng để gọi triều đại của anh em Nguyễn Nhạc, Nguyễn Lữ và Nguyễn Huệ để phân biệt với nhà Nguyễn của Nguyễn Ánh (vì cùng họ Nguyễn). Một trong những công tích lớn nhất của nhà Tây Sơn trong lịch sử dân tộc là đã tiến đến rất gần công cuộc thống nhất và đồng thời mở rộng lãnh thổ đất nước sau hàng trăm năm Việt Nam bị chia cắt.” (Theo https://vi.wikipedia.org).
Viết tập hợp \(A\) gồm tên các anh em nhà Tây Sơn.
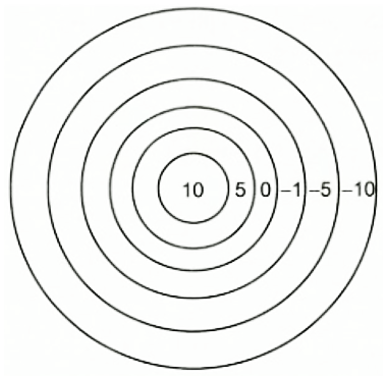
2. Trong trò chơi bắn bi vào các hình tròn vẽ trên mặt đất, bạn Quân đã bắn được 2 viên bi điểm 5; 3 viên bi điểm 0 và 3 viên bi điểm \( - 5.\) Bạn Hoàng đã bắn được 1 viên bi điểm 10; 2 viên bi điểm \( - 10\) và 2 viên bi điểm \( - 1.\) Hỏi bạn nào được cao điểm hơn?
3. Một nhân viên ở cửa hàng bán đồ ăn nhanh khi xếp số bánh ngọt vào các túi thì thấy rằng nếu xếp mỗi túi 10 chiếc, 12 chiếc hoặc 15 chiếc đều vừa đủ. Tính số bánh ngọt của cửa hàng biết rằng số bánh ngọt trong khoảng từ 100 đến 150 chiếc.
Lời giải
Hướng dẫn giải
1. Tập hợp \(A\) gồm tên các anh em nhà Tây Sơn là:
\(A = \{ \)Nguyễn Nhạc; Nguyễn Lữ; Nguyễn Huệ}.
2. Bạn Quân bắn được số điểm là:
\(2 \cdot 5 + 3 \cdot 0 + 3 \cdot \left( { - 5} \right) = 10 + \left( { - 15} \right) = 5\) (điểm).
Bạn Hoàng bắn được số điểm là:
\(1 \cdot 10 + 3 \cdot 5 + 3 \cdot \left( { - 10} \right) + 2 \cdot \left( { - 1} \right) = 10 + 15 - 20 - 2 = 3\) (điểm).
Do đó, bạn Hoàng được cao điểm hơn bạn Quân (5 điểm > 3 điểm).
3. Gọi \[x\] là số bánh ngọt của cửa hàng (chiếc, \(x \in \mathbb{N}*;\,\,100 \le x \le 150\))
Vì nếu xếp số bánh ngọt vào các túi, mỗi túi 10 chiếc, 12 chiếc, 15 chiếc đều vừa đủ nên\(x\,\, \vdots \,\,10,\,\,x\,\, \vdots \,\,12,\,\,x\,\, \vdots \,\,15.\)
Suy ra \(x\) là \(BC\left( {10,12,15} \right)\)
Ta có: \(10 = 2.5;\,\,\,\,12 = {2^2}.3;\,\,\,15 = 3.5\)
Do đó \(BCNN\left( {10,12,15} \right) = {2^2}.3.5 = 60\)
Suy ra \(BC\left( {10,12,15} \right) = B\left( {60} \right) = \left\{ {0;60;120;180;...} \right\}\)
Mà \(100 \le x \le 150\) nên \(x = 120\)
Vậy cửa hàng có 120 chiếc bánh ngọt.
Lời giải
Hướng dẫn giải
1. a) Trong các chữ cái trên, có 3 chữ cái có tâm đối xứng, đó là các chữ cái sau:
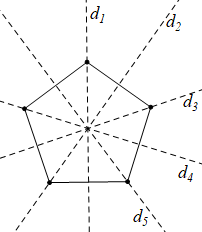
b) Hình ngũ giác đều có năm trục đối xứng
Các trục đối xứng được biểu diễn như hình vẽ:
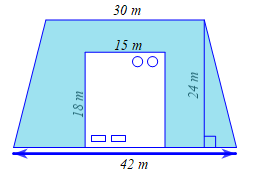
2. a) Diện tích khu đất làm nhà là: \(15.18 = 270\,\,\left( {{{\rm{m}}^2}} \right)\).
Vậy diện tích khu đất làm nhà là \(270\,\,{{\rm{m}}^2}.\)
b) Diện tích khu đất hình thang cân dùng để làm nhà và trồng cỏ là:
\(\frac{1}{2}\left( {30 + 42} \right).24 = 864\,\,\left( {{{\rm{m}}^2}} \right)\)
Diện tích dùng để trồng cỏ là:
\(864 - 270 = 594\,\,\left( {{{\rm{m}}^2}} \right)\).
Để gieo hết bãi cỏ thì cần số túi hạt giống là:
\(594:33 = 18\) (túi).
Vậy mỗi túi hạt giống cỏ gieo vừa đủ trên \(33\,\,{{\rm{m}}^2}\) đất thì cần 18 túi hạt giống để gieo hết bãi cỏ.
Lời giải
Hướng dẫn giải
Vì robot được lập trình cứ tiến 6 bước thì lùi 2 bước nên mỗi lượt thực hiện một lập trình, robot đi được quãng đường là: \(6 \cdot 5 - 2 \cdot 5 = 20{\rm{\;}}\left( {{\rm{dm}}} \right){\rm{.}}\)
Như vậy, mỗi lần thực hiện một lập trình robot đi được quãng đường \(20{\rm{\;dm}}\) và bước tổng \(6 + 2 = 8\) (bước).
Ta có: \(126:8 = 15\) dư 6.
Do đó để đến B thì robot đã thực hiện 15 lập trình và bước thêm 6 bước.
Khi đó, quãng đường robot đi được là: \(15 \cdot 20 + 6 \cdot 5 = 330{\rm{\;(dm)}}{\rm{.}}\)
Vậy khoảng cách từ A đến B dài 330 dm.
Nhắn tin Zalo