Giải chuyên đề Tin 12 Cánh diều Bài 2: Kiểu dữ liệu ngăn xếp có đáp án

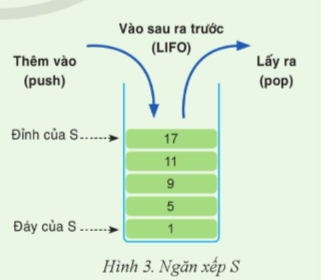
Lan xếp các đĩa CD thành một cọc (Hình 1). Mỗi lần lấy đĩa ra khỏi cọc, Lan sẽ lấy lần lượt tùng đĩa một từ trên xuống. Mỗi lần bổ sung. Lan cũng lần lượt xếp từng đĩa mới vào cọc. Em hãy: 

a) Cho biết với đĩa nằm ở đáy và đĩa nằm ở đỉnh cọc, đĩa nào được thêm vào cọc trước. 

b) So sánh quy tắc thực hiện thao tác thêm vào và lấy đĩa ra khỏi cọc với thao tác thêm vào và lấy ra phần tử khỏi hàng đợi đã được học ở bài trước.

Cho dãy A gồm 10 số nguyên lẻ 1, 3, 5, 7, 9, 11, 13, 15, 17, 19. Bạn Thái sẽ thực hiện một cách tuỳ ý các thao tác thêm vào và lấy ra trên ngăn xếp S ban đầu đang không có phần tử nào. Các thao tác thêm vào sẽ lấy ra lần lượt từng số trong dãy A để bổ sung vào ngăn xếp. Em hãy: 

a) Vẽ ngăn xếp S thu được sau khi Thái thực hiện hai thao tác thêm vào liên tiếp và một thao tác lấy ra. 

b) Cho biết Thái cần thực hiện những thao tác thêm vào và lấy ra theo thứ tự như thế nào để có thể thu được ngăn xếp S như ở Hình 3.

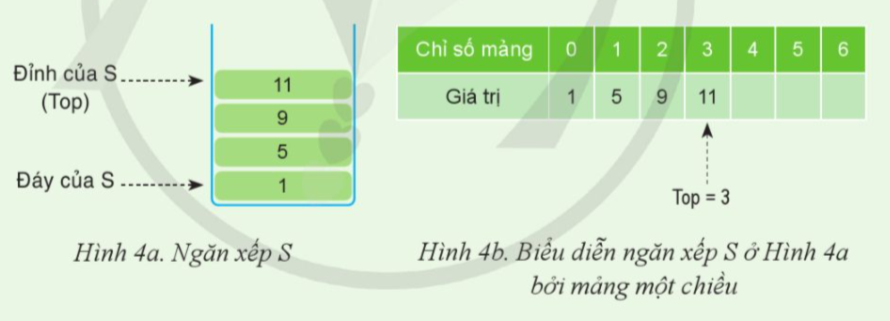
Để cài đặt ngăn xếp với hai thao tác thêm vào (push) và lấy ra (pop), ta có thể dùng mảng một chiều. Khi đó, các phần tử trong mảng sẽ là các phần tử đang có trong ngăn xếp.

Em hãy: 

a) Đọc hàm pop(S) ở Hình 8 và cho biết dấu ? cần được thay bằng gì. 

b) Đọc chương trình ở Hình 9 và cho biết kết quả thu được khi chạy chương trình.

c) Bổ sung hai câu lệnh temp=pop(stack) giống nhau vào cuối đoạn chương trình ở Hình 9 và cho biết kết quả thu được khi chạy chương trình. 

d) Viết hàm isEmptyStack(S) với tham số truyền vào là ngăn xếp S. Hàm trả về giá trị True nếu ngăn xếp S đang rỗng không chứa phần tử nào, ngược lại hàm trả về giá trị False. 

e) Sửa lại chương trình thu được khi thực hiện xong câu c) như sau: Thay mỗi câu lệnh temp = pop(stack) thành đoạn chương trình ở Hình 10. Cho biết kết quả thu được khi chạy chương trình.

Em hãy viết chương trình yêu cầu người sử dụng nhập năm số nguyên dương - bất kì từ bàn phím, sau đó in ra màn hình năm số này theo thứ tự đảo ngược của thứ tự nhập vào. Trong chương trình có sử dụng kiểu dữ liệu ngăn xếp và các thao tác đã học trên ngăn xếp. Ví dụ: Nhập vào năm số: 3, 1, 9, 17, 2. Kết quả in ra: 2, 17,9, 1, 3.

Trong các câu sau đây, những câu nào đúng khi nói về ngăn xếp? 

a) Cơ chế hoạt động của ngăn xếp là vào trước ra trước. 

b) Khác với kiểu dữ liệu hàng đợi, các phần tử trong ngăn xếp được truy cập một cách trực tiếp. 

c) Khi thêm ngăn xếp. một phần tử vào ngăn xếp, phần tử này sẽ được đặt ở đây của 

d) Có thể thêm một phần tử mới vào vị trí bất kì trong ngăn xếp 

e) Cơ chế hoạt động của ngăn xếp là vào sau ra trước. 

g) Có thể xoá một phần tử bất kì khỏi ngăn xếp bằng một thao tác lấy ra.