Câu hỏi:

12/07/2024 1,362

Cho đường tròn (O), P là một điểm cố định nằm trong (O) nhưng không trùng với tâm O. Một đường thẳng d thay đổi qua P cắt (O) tại A và B. Tìm quỹ tích trung điểm M của đoạn AB khi d quay quanh P.

Xem lời giải

Câu hỏi trong đề: Trắc nghiệm Chuyên đề toán 9 Chuyên đề 5: Cung chứa góc có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Phần thuận: (Hình 1)

Nối OM. Vì M là trung điểm của AB nên $OM ⊥ AB \Rightarrow \hat{POM} = 90 °$ , tức là M luôn nhìn đoạn OP dưới một góc vuông. Vậy M luôn thuộc đường tròn đường kính OP.

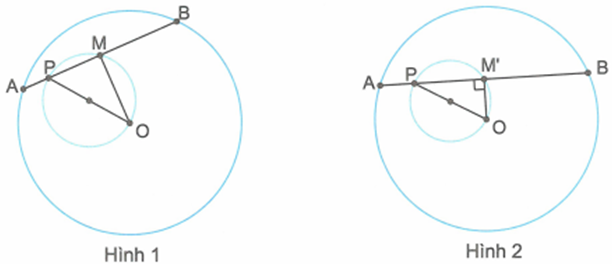
Cho đường tròn (O) , P là một điểm cố định nằm trong (O) nhưng không trùng với tâm O . (ảnh 1)

Giới hạn: Theo chứng minh trên thì mọi điểm M thuộc quỹ tích đều thuộc đường tròn đường kính OP.

Vị trí M trùng O tương ứng với trường hợp d đi qua O.

Như vậy, quỹ tích là cả đường tròn đường kính OP.

Phần đảo: (Hình 2)

Lấy một điểm M' bất kì thuộc đường tròn đường kính OP (M' khác O). Nối OM'. Qua M' kẻ đường thẳng d' vuông góc với OM' cắt (O) tại A' và B'. Do góc $\hat{O M^{'} P} = 90 °$ nên d' đi qua P.

Vì tam giác OA'B' cân tại O và OM' vuông góc với A'B' nên M' là trung điểm của A'B'.

Vậy M' là một điểm thuộc quỹ tích.

Kết luận: Quỹ tích là đường tròn đường kính OP.

Chú ý: Nếu P là một điểm nằm ngoài đường tròn thì quỹ tích sẽ chỉ là phần đường tròn đường kính OP nằm bên trong (O). Như vậy, phần đảo và phần giới hạn có ý nghĩa nói chung không thể bỏ qua.

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho một đường tròn (O) và dây AB cố định, điểm C chuyển động trên cung lớn AB (C khác A và B). Chứng minh rằng tâm I của đường tròn nội tiếp tam giác ABC chuyển động trên một cung tròn cố định.

Xem đáp án

Lời giải

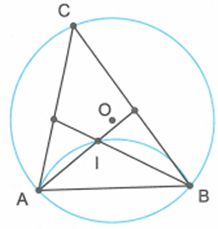
Cho một đường tròn (O) và dây AB cố định, điểm C chuyển động trên cung lớn AB ( C khác A và B ). (ảnh 1)

Vì dây AB cố định nên

\hat{A C B} = \frac{1}{2} s đ \overset{⏜}{A B}

không đổi.

Đặt $\hat{A C B} = α$ . Ta có:

$\hat{B A C} + \hat{A B C} + \hat{A C B} = 180 °$ (tổng ba góc trong một tam giác).

$\Rightarrow \hat{B A C} + \hat{A B C} = 180 ° - \hat{A C B} = 180 ° - α$ .

Vì I là tâm đường tròn nội tiếp tam giác ABC nên AI, BI lần lượt là tia phân giác của hai góc A và B. Suy ra

$\hat{I A B} = \frac{1}{2} \hat{B A C}; \hat{I B A} = \frac{1}{2} \hat{A B C} \Rightarrow \hat{I A B} + \hat{I B A} = \frac{1}{2} (\hat{B A C} + \hat{A B C}) = 90 ° - \frac{α}{2}$

Lại có: $\hat{A I B} + \hat{I A B} + \hat{I B A} = 180 °$ (tổng ba góc trong một tam giác).

$\Rightarrow \hat{A I B} = 180 ° - (\hat{I A B} + \hat{I B A}) = 180 ° - (90 ° - \frac{α}{2}) = 90 ° + \frac{α}{2}$ không đổi.

Vì AB cố định, I thuộc nửa mặt phẳng chứa cung lớn AB có bờ là đường thẳng AB nên I luôn chuyển động trên cung chứa góc $90 ° + \frac{α}{2}$ dựng trên đoạn AB.

Câu 2

Cho nửa đường tròn (O;R) đường kính AB. Vẽ dây MN = R (điểm M ở trên cung $\overset{⏜}{A N}$ ). Hai dây AN và BM cắt nhau tại I. Hỏi khi dây MN di động thì điểm I di động trên đường nào?

Xem đáp án

Lời giải

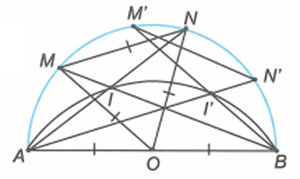
Cho nửa đường tròn (O; R) đường kính AB . Vẽ dây MN = R (điểm M ở trên cung AN ). (ảnh 1)

Phần thuận: Tam giác MON đều (vì

O M = O N = M N = R

\Rightarrow \hat{M O N} = 60 ° \Rightarrow s đ \overset{⏜}{M N} = 60 ° \Rightarrow s đ \overset{⏜}{A M} + s đ \overset{⏜}{N B} = 180 ° - 60 ° = 120 ° \Rightarrow \hat{N I B} = \frac{1}{2} (s đ \overset{⏜}{A M} + s đ \overset{⏜}{N B}) = 60 °

Ta có: $\hat{A I B} = 180 ° - \hat{N I B} = 120 °$ (hai góc kề bù).

Do AB cố định nên quỹ tích điểm I là cung chứa góc $120 °$ dựng trên đoạn AB.

Phần đảo: Trên cung chứa góc $120 °$ dựng trên đoạn AB, lấy điểm I'. AI' và BI' lần lượt cắt nửa đường tròn (O) tại N' và M'. Khi đó $\hat{A I^{'} B} = 120 ° \Rightarrow \hat{B I^{'} N^{'}} = 60 ° \Rightarrow \hat{M^{'} O N^{'}} = 60 °$ .

Suy ra tam giác M'O'N' đều. Do đó M'N' = R.

Vậy I' là một điểm thuộc quỹ tích.

Kết luận: Quỹ tích các điểm I là cung chứa góc $120^{\circ}$ dựng trên đoạn AB.

Câu 3

Cho nửa đường tròn đường kính AB cố định. C là một điểm trên nửa đường tròn, trên dây AC kéo dài lấy điểm D sao cho CD = CB.
a) Tìm quỹ tích các điểm D khi C chạy trên nửa đường tròn đã cho.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho nửa đường tròn đường kính AB và một dây AC quay quanh A. Trên nửa mặt phẳng bờ AC không chứa B ta vẽ hình vuông ACDE. Hỏi:

a) Điểm D di động trên đường nào?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hình vuông ABCD. Trên cạnh BC lấy điểm E, trên tia đối của tia CD lấy điểm F sao cho CE = CF. Gọi M là giao điểm của hai đường thẳng DE và BF. Tìm quỹ tích của điểm M khi E di động trên cạnh BC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

b) Điểm E di động trên đường nào?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho đường tròn (O), P là một điểm cố định nằm trong (O) nhưng không trùng với tâm O. Một đường thẳng d thay đổi qua P cắt (O) tại A và B. Tìm quỹ tích trung điểm M của đoạn AB khi d quay quanh P.

Cho một đường tròn (O) và dây AB cố định, điểm C chuyển động trên cung lớn AB (C khác A và B). Chứng minh rằng tâm I của đường tròn nội tiếp tam giác ABC chuyển động trên một cung tròn cố định.

Cho nửa đường tròn (O;R) đường kính AB. Vẽ dây MN = R (điểm M ở trên cung AN⏜). Hai dây AN và BM cắt nhau tại I. Hỏi khi dây MN di động thì điểm I di động trên đường nào?

Cho nửa đường tròn đường kính AB cố định. C là một điểm trên nửa đường tròn, trên dây AC kéo dài lấy điểm D sao cho CD = CB. a) Tìm quỹ tích các điểm D khi C chạy trên nửa đường tròn đã cho.

Cho nửa đường tròn đường kính AB và một dây AC quay quanh A. Trên nửa mặt phẳng bờ AC không chứa B ta vẽ hình vuông ACDE. Hỏi: a) Điểm D di động trên đường nào?

Cho hình vuông ABCD. Trên cạnh BC lấy điểm E, trên tia đối của tia CD lấy điểm F sao cho CE = CF. Gọi M là giao điểm của hai đường thẳng DE và BF. Tìm quỹ tích của điểm M khi E di động trên cạnh BC.

b) Điểm E di động trên đường nào?

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho nửa đường tròn (O;R) đường kính AB. Vẽ dây MN = R (điểm M ở trên cung $\overset{⏜}{A N}$ ). Hai dây AN và BM cắt nhau tại I. Hỏi khi dây MN di động thì điểm I di động trên đường nào?

Cho nửa đường tròn đường kính AB cố định. C là một điểm trên nửa đường tròn, trên dây AC kéo dài lấy điểm D sao cho CD = CB.
a) Tìm quỹ tích các điểm D khi C chạy trên nửa đường tròn đã cho.

Cho nửa đường tròn đường kính AB và một dây AC quay quanh A. Trên nửa mặt phẳng bờ AC không chứa B ta vẽ hình vuông ACDE. Hỏi:

a) Điểm D di động trên đường nào?