Quảng cáo
Trả lời:
Tứ giác HEBF nội tiếp (do BEH = BFH = 90)
=> BFE = BHE (cùng chắn BE).
Tứ giác CDHF nội tiếp (do CDH = CFH = 90) => CFD = CHD.
Mà BHE = CHD nên BFE = CFD.
Mặt khác: BFE +EFA = 90 và CFD + DFA = 90. Do đó EFA = DFA. Vậy FH là tia phân giác của góc EFD.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
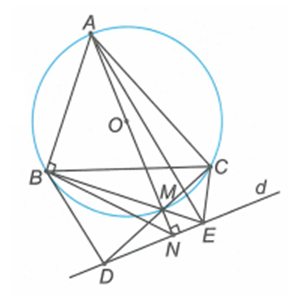
Kẻ đường kính AM cắt d tại N. Ta có ANE = ABE = 90 nên tứ giác ABNE nội tiếp, suy ra BEN = BAN.
Mặt khác BAN = BCM, do đó BCM = BEN hay BCD = BED.
Vậy B , C , D , E cùng thuộc một đường tròn.
Lời giải
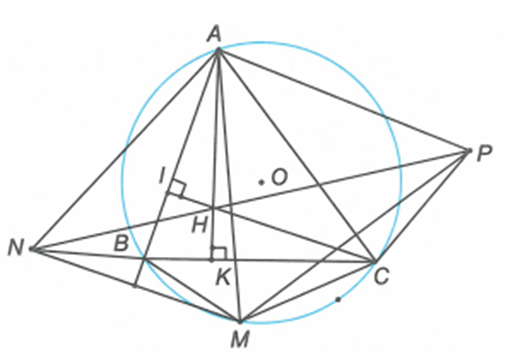
Giả sử các đường cao của tam giác là AK, CI. Để chứng minh AHCP nội tiếp ta sẽ chứng minh AHC + APC = 120.
Ta có: AHC = IHK (đối đỉnh),
APC = AMC = ABC (do tính đối xứng và góc nội tiếp cùng chắn một cung).
Lại có tứ giác BIHK là tứ giác nội tiếp nên ABC + IHK = 180 => AHC + APC = 180.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.