Câu hỏi:

14/09/2022 559

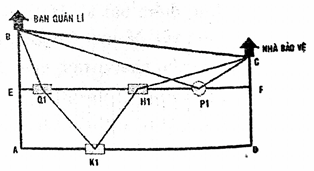
Cho hình vuông ABCD. Hãy xác định đường thẳng đi qua tam hình vuông cắt các cạnh đối AD và BC sao cho tổng khoảng cách từ bốn đỉnh của hình vuông đến đường thẳng đó là

a) Lớn nhất

Xem lời giải

Câu hỏi trong đề: Trắc nghiệm Chuyên đề Toán 9 Chuyên đề 9: Bài toán thực tế Hình học có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

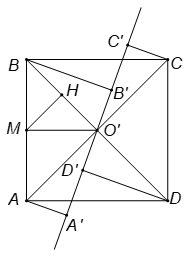
Cho hình vuông ABCD. Hãy xác định đường thẳng đi qua tam hình vuông cắt các cạnh đối AD và (ảnh 1)

Gọi d là đường thẳng qua tâm O' của hình vuông, m là tổng các khoảng cách từ bốn đỉnh của hình vuông đến d.

Xét trường hợp đường thẳng d cắt hai cạnh đối AD và BC. Kẻ $A A^{'}, B B^{'}, C C^{'}, D D^{'}$ vuông góc với d.

Ta thấy $m = A A^{'} + B B^{'} + C C^{'} + D D^{'} = 2 (A A^{'} + B B^{'})$ .

Gọi M là trung điểm của AB, N là trung điểm của A'B'. Ta có $M N ⊥ A^{'} B^{'}$ và MN là đường trung bình của hình thang ABB'A' nên $A A^{'} + B B^{'} = 2 M N$ .

Do đó: m lớn nhất $\Leftrightarrow M N$ lớn nhất.

m nhỏ nhất $\Leftrightarrow M N$ nhỏ nhất.

a) Ta có $M N \leq M O^{'}$ (không đổi) nên MN lớn nhất.

$\Leftrightarrow N \equiv O^{'} \Leftrightarrow d ∥ A B$ .

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Đường quốc lộ và đường ống dân dầu cắt nhau một góc nhỏ hơn 45⁰, trong góc này có một bãi đỗ các ô tô của xí nghiệp vận tải. Xây trạm cung cấp xăng ở vị trí nào trên đường ống để các loại xe xuất phát từ bãi đỗ xe đến lấy xăng rồi ra đường quốc lộ với đường đi ngắn nhất.

Xem đáp án

Lời giải

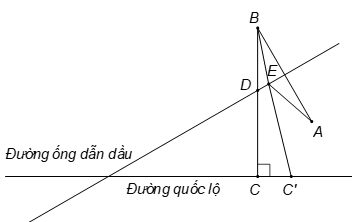
Đường quốc lộ và đường ống dân dầu cắt nhau một góc nhỏ hơn 45 độ, trong góc này có một (ảnh 1)

Ta thấy điểm dân cư A và điểm lối thoát ra đường quốc lộ nằm cùng một phía đường ống dẫn đầu. Tương tự như ví dụ 1, ta lấy điểm B đối xứng với điểm A qua đường ống dẫn dầu.

Từ điểm B hạ đường vuông góc xuống đường quốc lộ, đường ta vừa hạ sẽ cắt đường ống dẫn dầu tại D, có chân đường vuông góc tại C. Điểm D chính là nơi ta xây trạm cung cấp xăng và đoạn đường $A D + D C$ là đoạn đường ngắn nhất ta phải mở.

Thật vậy, gọi E là điểm bất kì trên đường ống dẫn dầu, C' là điểm bất kì trên đường quốc lộ. Ta có:

$A E + E C^{'} = B E + E C^{'} \geq B C^{'} \geq B C = B D + D C = A D + D C$

(do BC là đoạn đường ngắn nhất từ B đến đường quốc lộ).

Câu 2

Cho tam giác nhọn ABC. Hãy nội tiếp trong tam giác ABC một tam giác có chu vi bé nhất.

Xem đáp án

Lời giải

Cho tam giác nhọn ABC. Hãy nội tiếp trong tam giác ABC một tam giác có chu vi bé nhất. (ảnh 1)

Xét những tam giác nội tiếp PMN có đỉnh P cố định trên đáy BC.

Lấy $P_{1}, P_{2}$ đối xứng của P qua AB và AC, $P_{1}, P_{2}$ cắt AB, AC tại N và M. PMN là tam giác cần dựng vì chu vi tam giác PMN bằng $P N + N M + M P = P_{1} P_{2} < P_{1} N^{'} + N^{'} M^{'} + M^{'} P_{2}$ bằng
chu vi tam giác PM'N.

Như vậy, chúng ta cần phải tìm vị trí P để $P_{1} P_{2}$ là bé nhất.

Do $P_{1} P_{2}$ là đáy tam giác cân $A P_{1} P_{2}$ có $\hat{P_{1} A P_{2}} = 2 \hat{B A C}$ không đổi. Suy ra $P_{1} P_{2}$ đạt giá trị nhỏ nhất khi cạnh bên $A P_{1} = A P_{2} = A P$ bé nhất khi $A P ⊥ B C$ . Hay AP là đường cao của tam giác ABC.

Tương tự lập luận trên lấy điểm N thuộc AB cố định hay M thuộc AC cố định ta đi đến kết luận chu vi tam giác ABC bé nhất khi CN và BM là các đường cao của tam giác ABC.

Câu 3

Có hai điểm dân cư cùng phía bên cạnh một dòng sông. Người ta muốn xây dựng một trạm cung cấp nước lấy từ dòng sông và qua xử lí cung cấp cho hai điểm dân cư nói trên. Vậy phải đặt trạm xử lí nước tại điểm nào trên bờ sông để độ dài đường ống dẫn nước từ đó tới hai điểm dân cư là nhỏ nhất?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Trong lòng một con sông rộng có một hòn đảo hình tròn. Người ta muốn xây dựng những bến đỗ cho các tàu chở khách du lịch để chở khách từ đảo lên một bờ rồi nhận khách, đi sang ngay bờ bên kia nhận khách tiếp rồi chở về đảo hoặc ngược lại. Phải đặt các bến ở đâu để đường đi trên sông là ngắn nhất, biết rằng đường thẳng hai bờ sông kéo dài cắt nhau tại O tạo thành một góc nhọn.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Một mảnh đất hình tam giác nhọn ABC nằm ở vị trí giao nhau của ba con sông. Trong mảnh đất này có hai nhà máy D và E. Tàu chở hàng thả hàng ở ba vị trí $M, K, L$ lần lượt nằm trên các cạnh $A C, A B, B C$ của tam giác ABC. Hãy tìm các vị trí bỏ hàng $M, K, L$ để quãng đường đi từ D đến M, đến K đến L rồi đến E là nhỏ nhất.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Có hai kho chứa xăng hình tròn ở cùng một phía đối với đường quốc lộ. Người ta muốn xây dựng một trạm cung ứng và phân phối xăng bên đường quốc lộ nối với hai đường ống nối tới hai bồn xăng là ngắn nhất.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho hình vuông ABCD. Hãy xác định đường thẳng đi qua tam hình vuông cắt các cạnh đối AD và BC sao cho tổng khoảng cách từ bốn đỉnh của hình vuông đến đường thẳng đó là a) Lớn nhất

Bình luận

Cho tam giác nhọn ABC. Hãy nội tiếp trong tam giác ABC một tam giác có chu vi bé nhất.

Có hai kho chứa xăng hình tròn ở cùng một phía đối với đường quốc lộ. Người ta muốn xây dựng một trạm cung ứng và phân phối xăng bên đường quốc lộ nối với hai đường ống nối tới hai bồn xăng là ngắn nhất.

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hình vuông ABCD. Hãy xác định đường thẳng đi qua tam hình vuông cắt các cạnh đối AD và BC sao cho tổng khoảng cách từ bốn đỉnh của hình vuông đến đường thẳng đó là

a) Lớn nhất