Câu hỏi:
11/07/2024 449
Một ô tô C, một xe đạp B và điểm cố định A đang ở vị trí tạo thành tam giác vuông tại B. Ô tô và xe đạp khởi hành cùng một lúc đi về phía A theo các cạnh của tam giác ABC. Sau khi ô tô đi được 25km thì tam giác tạo bởi điểm A, ô tô C, xe đạp B là tam giác đều. Khi ô tô đến A thì xe đạp còn phải đi 12km nữa mới đến A. Tìm khoảng cách ban đầu của ô tô và xe đạp.
Một ô tô C, một xe đạp B và điểm cố định A đang ở vị trí tạo thành tam giác vuông tại B. Ô tô và xe đạp khởi hành cùng một lúc đi về phía A theo các cạnh của tam giác ABC. Sau khi ô tô đi được 25km thì tam giác tạo bởi điểm A, ô tô C, xe đạp B là tam giác đều. Khi ô tô đến A thì xe đạp còn phải đi 12km nữa mới đến A. Tìm khoảng cách ban đầu của ô tô và xe đạp.
Quảng cáo
Trả lời:
Giải bởi Vietjack
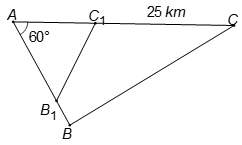
Góc A của tam giác vuông ABC với góc A là góc của tam giác đều là một góc.
Vậy .
Giả sử lúc đầu (km). Vậy (km).
Ta có: .
Gọi là vận tốc ô tô; là vận tốc xe đạp. Ta có:
Hệ phương trình này đưa đến phương trình
, .
Giải phương trình ta được x = 40.
Vì (km).
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
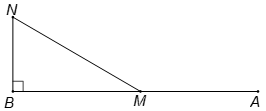
Gọi M là vị trí xe mô tô sau khi khởi hành t (h) và
N là vị trí xe đạp sau khi khởi hành t (h).
Ta có: .
.
Sử dụng định lí Pythagore, ta được:
.
Vậy MN ngắn nhất khi 3,6 (h) 3 giờ 36 phút.
Lời giải
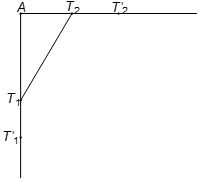
Gọi (km/h) là vận tốc của thuyền 1,
(km/h) là vận tốc của thuyền 2.
và là vị trí của thuyền 1, 2 sau 30 phút.
và là vị trí của thuyền 1, 2 sau 15 phút nữa.
Theo giả thiết: .
Đưa đến hệ: dẫn đến .
Giải phương trình ta được (km/h) thoả mãn bài toán
Vậy vận tốc thuyền 1 là 24 (km/h) và vận tốc thuyền 2 là 18 (km/h).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận